План скоростей и ускорений — Лекции и примеры решения задач технической механики
Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.
Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное – движение данной точки относительно той, движение которой принято за переносное:
На плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана.
На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает. Отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек.
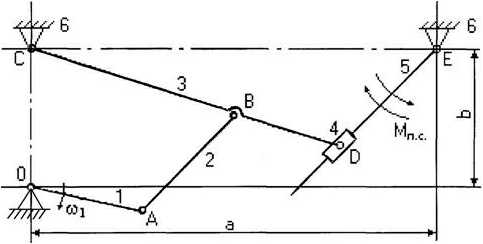
Рисунок 1 – Кинематическая схема плоского рычажного механизма
Рассмотрим построение планов для механизма, представленного на рисунке 1. Вначале рассматривается начальный механизм, а далее решение ведется по группам Ассура в порядке их присоединения.
Начальный механизм:
Здесь
По вычисленному значению VA выбираем масштаб плана скоростей KV и из произвольного полюса откладываем отрезок va изображающий эту скорость:
Можно также назначать отрезок va а масштаб KV вычислять:
Группа Ассура второго класса 1-го вида (звенья 2, 3):
Истинные значения (в м/с) относительных скоростей VBA и VBC определяются после построения плана умножением соответствующих отрезков (в мм) на масштаб плана:
а зная их, можно определить и угловые скорости звеньев 2 и 3:
Скорость точки D на плане скоростей можно определить по подобию. (Если известны скорости двух точек одного и того же звена, то скорость любой третьей точки этого же звена можно определить, построив на плане скоростей фигуру, подобную фигуре, образованной этими же буквами на звене механизма). Точки С, В , D на звене 3 лежат на одной прямой. На плане строим отрезок сd, соблюдая условие подобия:
Группа Ассура второго класса 3-го вида (звенья 4,5) :
где D5 — точка, находящаяся на звене 5 под точкой D. После определения скорости движения точки D
Примечание: в данном случае размер DE является величиной переменной (т.е. в задании он отсутствует), поэтому в каждом положении механизма он определяется через отрезок на чертеже и масштаб длин.
План ускорений строится в таком же порядке.
Начальный механизм
Ускорение точки A состоит только из нормальной составляющей, т.к. задана постоянная угловая скорость первого звена (ω1=соnst):
По вычисленному значению ускорения точки A выбирается масштаб плана ускорений и определяется отрезок на плане, соответствующий этому ускорению (или вычисляется масштаб плана ускорений по выбранному отрезку, изображающему ускорение точки A):
Здесь точка w – полюс плана ускорений.
Группа Ассура (звенья 2,3) второго класса 1-го вида:
После построения определяются aτBA и aτBC, по которым можно вычислить угловые ускорения звеньев 2 и 3:
Ускорение точки D определяем по подобию так же, как определяли скорость этой точки:
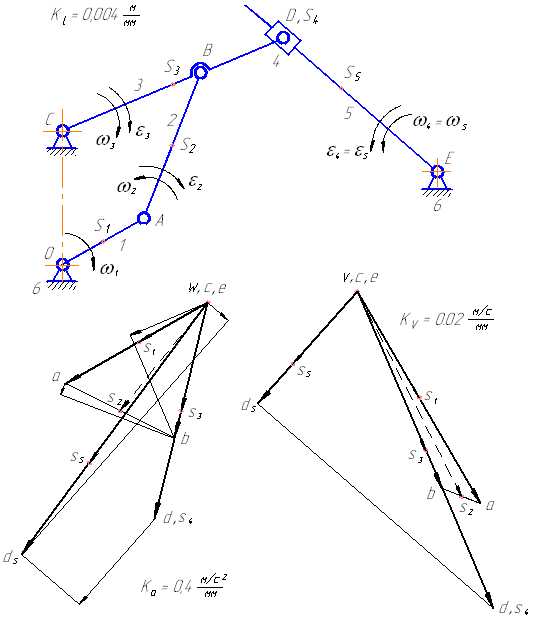
Рисунок 5 – Планы скоростей и ускорений для заданного положения механизма
Группа Ассура (звенья 4,5) второго класса 3-го вида:
Для определения направления akD5D надо вектор VD5D повернуть на 90° в направлении ω5. Угловые ускорения:
При силовом расчете необходимо иметь ускорения центров масс (asi), которые на плане ускорений определяются методом подобия.
Планы скоростей и ускорений для первого положения заданного механизма приведены на рисунке 5.
Уравнение планов скоростей и ускорений для каждой группы Ассура приведены в таблице 1.
Таблица 1 – Кинематический анализ групп Ассура II класса методом планов
Пример расчета механизма с поступательно движущимся выходным звеном >
Курсовой проект по ТММ >
isopromat.ru
ТММ
СОДЕРЖАНИЕ:
КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА. 2
Задание на курсовой проект. 2
Структурный анализ механизма. 2
План положений механизма. Построение графиков. 3
Построение плана скоростей. 3
Построение плана ускорений. 5
кинетостатический анализ рычажного механизма 6
Кинетостатический расчет группы звеньев 2 – 3. 7
Кинетостатический расчет ведущего звена. 8
Рычаг Н.Е. Жуковского. 8
Список Литературы 10
КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА.
Задание на курсовой проект.
В курсовом проекте необходимо рассчитать кривошипно-шатунный механизм по следующим исходным данным:
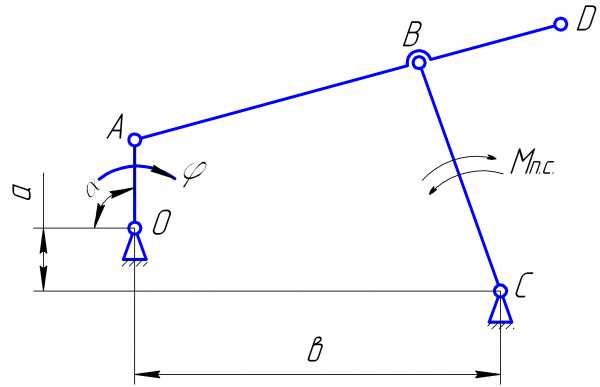
Рис. 1. Схема кривошипно-шатунного механизма.
Число оборотов пОА=120 об/мин
Длина кривошипа ОА=0,06м
Длина шатуна АВ=0,14 м
Длина ДВ=0,03 м
Длина СВ=0,20м
а=0,02 м
в=0,18м
Угол =60
Момент полезного сопротивления Мп.с.=60Н*м
Структурный анализ механизма.
Плоский кривошипно-шатунный механизм состоит из 3-х подвижных звеньев и 2-х неподвижных (стоек). Механизм имеет вращательные кинематические пары пары 5-го класса, где p5=3.Степень подвижности механизма определяем по формуле Чебышева:
где 3 – количество свободных движений отдельно взятого звена на плоскости;
n=3 – число подвижных звеньев;
2 – число условий связи (ограничений), накладываемых парами пятого класса;
р5 =3 – число пар пятого класса;
р4 =2 – число пар четвертого класса.
План положений механизма. Построение графиков.
В масштабе длин 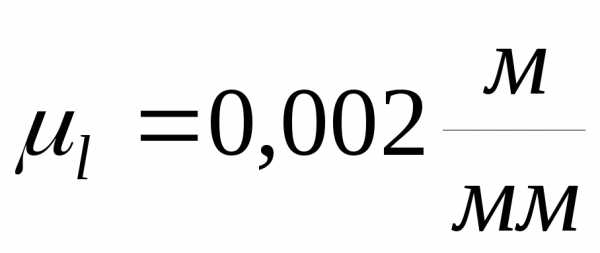 строим планы положений механизма для
двенадцати положений в предположении
того, что угловая скорость ведущего
звена (кривошипа ОА) постоянна (1=const).
Кривошип ОА изображаем в 12 положениях
через каждые 30,
начиная с положения, соответствующего
крайнему правому положению коромысла
СВ. Данное положение принимаем за начало
рабочего хода ведомого звена. Затем
изображаем все остальные звенья механизма
в положениях, соответствующих положениям
кривошипа.
строим планы положений механизма для
двенадцати положений в предположении
того, что угловая скорость ведущего
звена (кривошипа ОА) постоянна (1=const).
Кривошип ОА изображаем в 12 положениях
через каждые 30,
начиная с положения, соответствующего
крайнему правому положению коромысла
СВ. Данное положение принимаем за начало
рабочего хода ведомого звена. Затем
изображаем все остальные звенья механизма
в положениях, соответствующих положениям
кривошипа.
Строим график зависимости угла поворота коромысла, от угла поворота кривошипа. Определяем масштабы построений:
Масштаб для оси угловых перемещений кривошипа:.
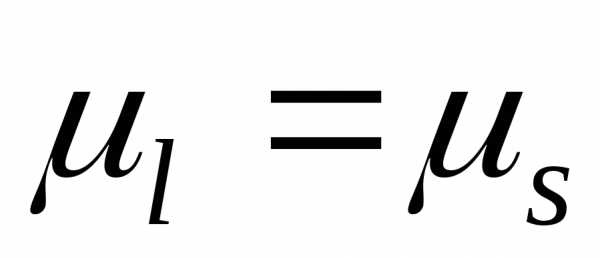 — т.к. при построение
диаграммы перемещений, масштаб построения
не изменился.
— т.к. при построение
диаграммы перемещений, масштаб построения
не изменился.
Определим  :
:
Определим  : м
: м
Определим 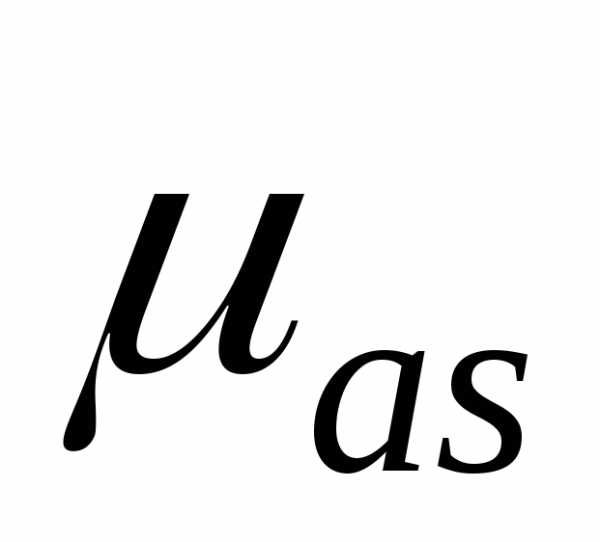 : мc-2/мм
: мc-2/мм
Построение плана скоростей.
Скорость точки. А:
Из полюса Р откладываем отрезок Ра звену ОА направленный в сторону вращения кривошипа ОА (по касательной к траектории движения точки А) длиной 50 мм изображающий вектор скорости точки А.
Масштаб плана скоростей:
Скорость точки В определяется системой уравнений:
Линии действия неизвестных скоростей известны, они будут перпендикулярны звеньям АВ и СВ соответственно. По этому данную систему уравнений можно решить графически.
Через конец вектора скорости точки А проводим линию действия вектора скорости VBА. Из полюса проводим линию действия вектора скорости VBС. Точка пересечения этих линий дают нам вектор скорости точки В. Измерив его длину и умножив на масштаб, получим скорость точки В:
м/с.
м/с.
Скорость точки D находим аналогично:
Точка d на плане скоростей будет лежать на продолжении отрезка аb. Длина отрезка аd на плане:
Соединив точку d с полюсом, найдем абсолютную скорость точки D.
м/с.
Найдем скорость VS2A:
Минимальная скорость первого звена:
Угловые скорости звеньев:
;
;
;
Скорости точек в рабочем положении.
VA | VB | VD | VS1 | VS2 | VS3 | VВА | VDA | VS2А | |
Длины отрезков плана скоростей, мм | 50 | 55 | 56 | 25 | 52 | 27,5 | 24 | 27,16 | 12,348 |
Скорости точек, м/с | 1,458 | 1,603 | 1,658 | 0,729 | 1,521 | 0,8 | 0,7 | 0,792 | 0,36 |
Построение плана ускорений.
Планы ускорений также строим для рабочего положения.
Ускорение точки А:
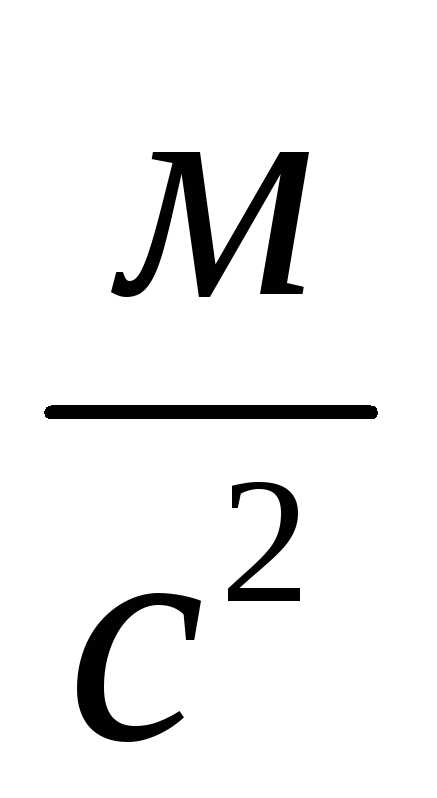 ,
,
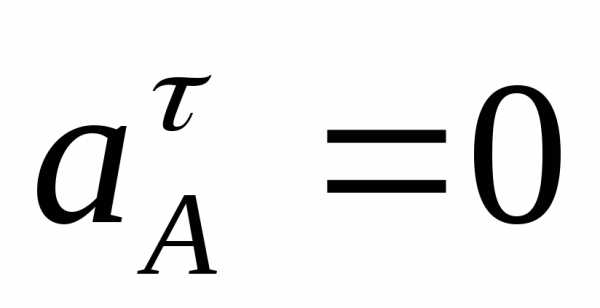 ,
потому что
,
потому что
Из полюса
откладываем отрезок  длиной 50 мм изображающий вектор ускорения
точки А.
Направление вектора от точки А к точке
О.
длиной 50 мм изображающий вектор ускорения
точки А.
Направление вектора от точки А к точке
О.
Масштаб плана ускорений:
Для нахождения ускорения точки В составляем систему уравнений:
Зная угловые скорости, можем определить нормальные составляющие ускорений:
, 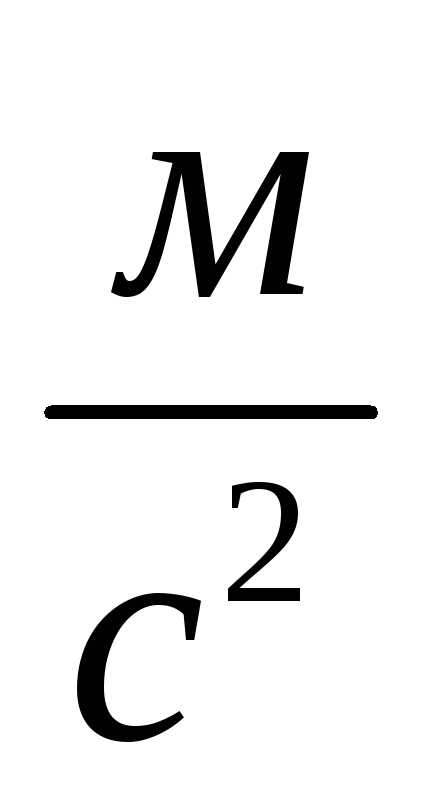
,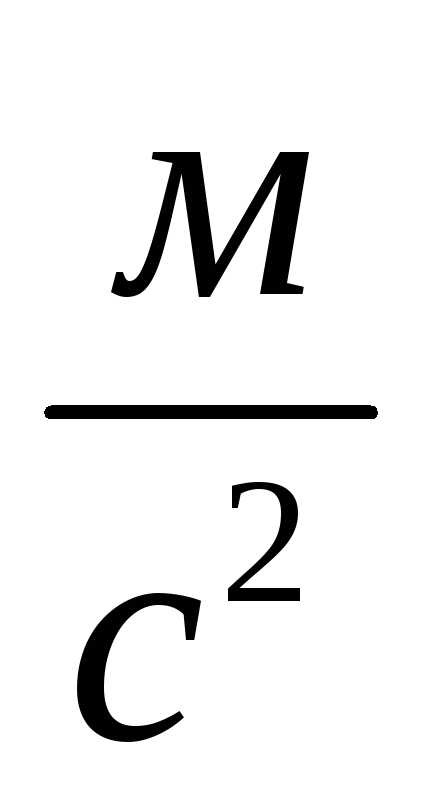
Согласно векторным
уравнениям откладываем 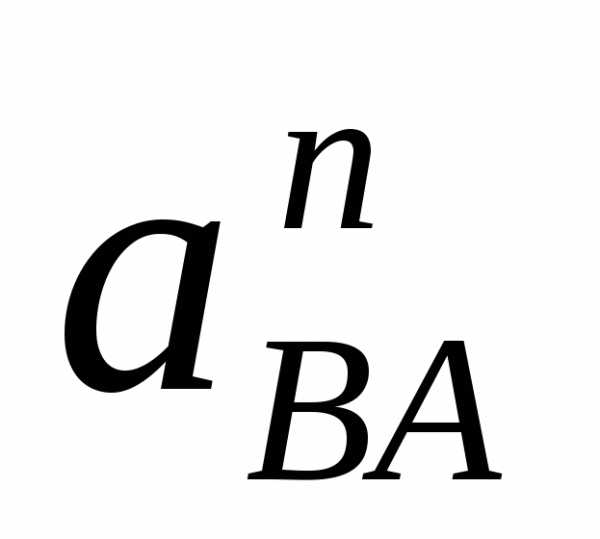 и
и 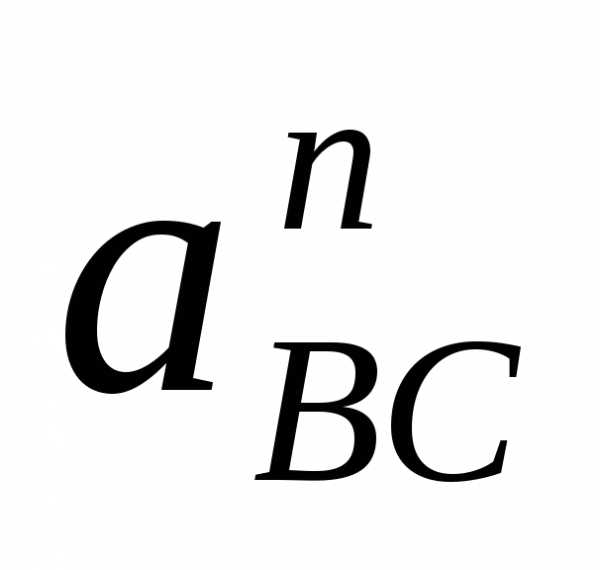 и перпендикулярно к ним откладываем
векторы тангенциальных ускорений, точка
пересечения которых дает нам абсолютный
вектор ускорения точки В.
и перпендикулярно к ним откладываем
векторы тангенциальных ускорений, точка
пересечения которых дает нам абсолютный
вектор ускорения точки В.
м/с2.
, 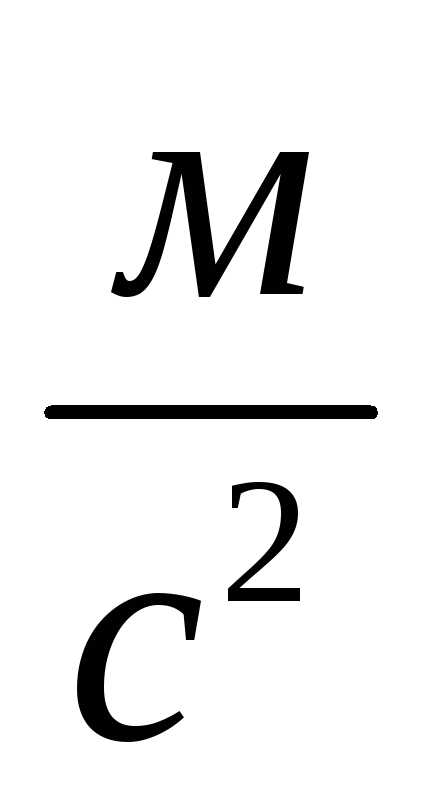
,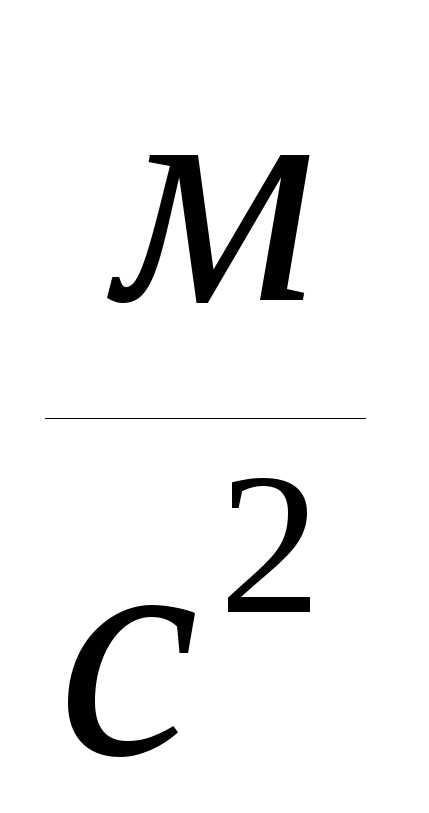
Угловые ускорения звеньев.
с-2;
с-2;
Ускорения точек в рабочем положении.
aA | aB | anBA | aBA | anBС | aBС | as1 | as2 | as3 | |
Длины отрезков плана ускорений, мм | 50 | 22 | 4,879 | 4,879 | 20 | 4 | 25 | 23 | 11 |
Ускорения точек, м/с2 | 17,706 | 7,791 | 1,728 | 11,686 | 7,114 | 1,417 | 8,853 | 8,145 | 3,895 |
Ускорения центров масс звеньев.
м/с2;
м/с2;
м/с2;
Для кинетостатического расчета определяем все активные силы:
Принимаем удельную массу одного метра звена .
Массы звеньев кг.
Масса 1-го звена кг;
Масса 2-го звена кг;
Масса 3-го звена кг;
Силы тяжести Н.
Сила тяжести 1-го звена Н;
Сила тяжести 2-го звена Н;
Сила тяжести 3-го звена Н;
Силы инерции Н,
Сила инерции 1-го звена Н;
Сила инерции 2-го звена Н;
Сила инерции 3-го звена Н;
Моменты сил инерции Нм,
Момент силы инерции 2-го звена Нм;
Момент силы инерции 3-го звена Нм;
Момент полезного сопротивления МП.с.=60 Н/м.
Кинетостатический расчет группы звеньев 2 – 3.
Строим
группы Асура 2 и 3 звеньев в масштабе 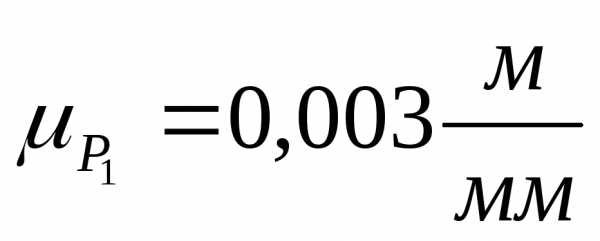 ,
в соответствующих точках прикладываем
все активные силы: силы тяжести, силы
инерции, моменты сил инерции. Также
прикладываем реакции R0,3 и R1,2,
которые требуется определить. Определяем
плечи действия активных сил относительно
точки В:
,
в соответствующих точках прикладываем
все активные силы: силы тяжести, силы
инерции, моменты сил инерции. Также
прикладываем реакции R0,3 и R1,2,
которые требуется определить. Определяем
плечи действия активных сил относительно
точки В:
м;
м;
м;
м;
Составляем уравнения моментов всех сил действующих на 3 звено относительно точки В:
;
;
Составляем уравнения моментов всех сил действующих на 2 звено относительно точки В:
;
Составляем векторное уравнение равновесия всех сил, действующих на группу звеньев 2-3:

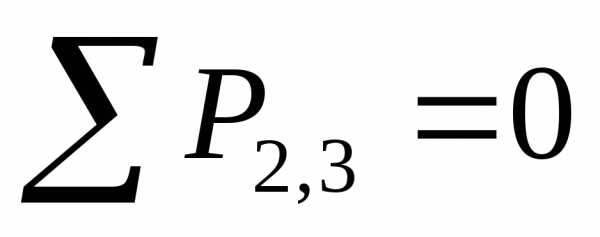 ;
;
В
выбранном масштабе сил строим план сил, указанных в уравнении.
Из плана сил определяем 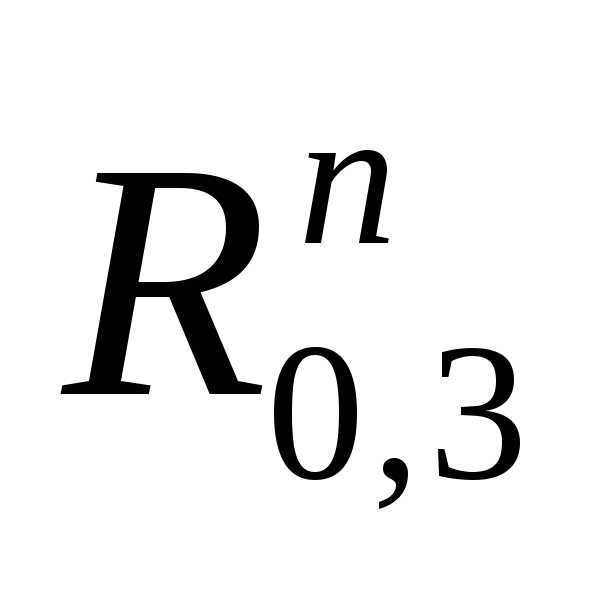 и
и 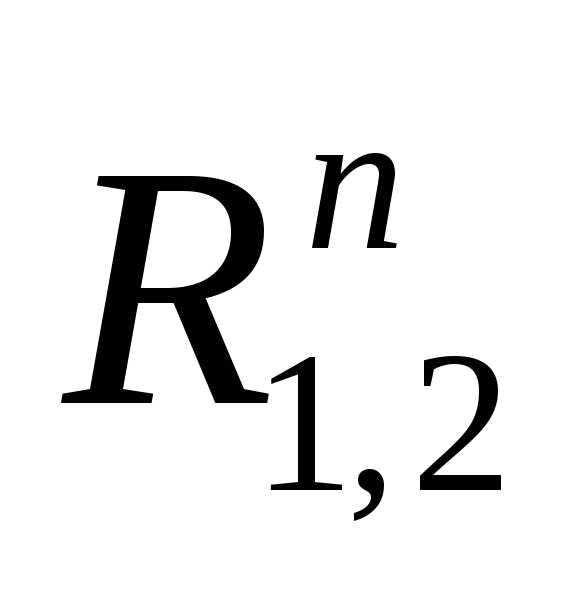 :
:

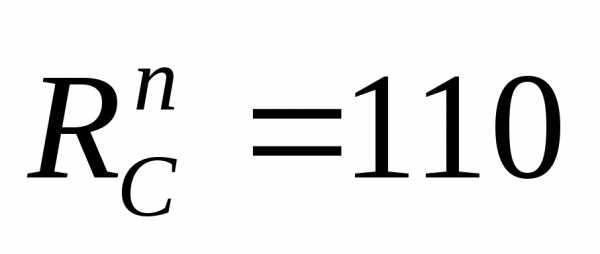 H;
H;
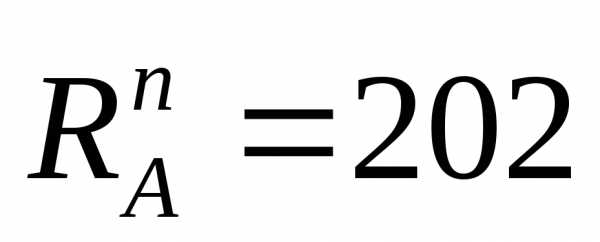 H.
H.
Исходя из суммы векторов нормальной и тангенциальной реакции опоры находим значения сил R0,3 и R1,2:
H;
H.
Кинетостатический расчет ведущего звена.
Строим
ведущее звено в масштабе 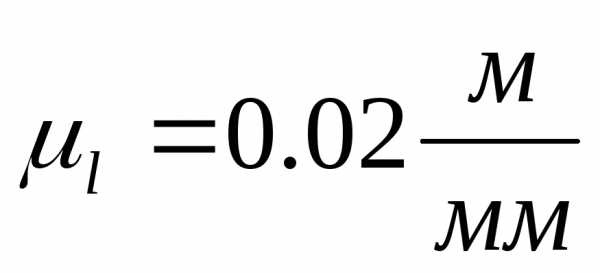 ,
в соответствующих точках прикладываем
все активные силы: силы тяжести, силы
инерции, моменты сил инерции и реакцию
опоры R2,1.
Также прикладываем реакцию R0,1,
которую требуется определить. Реакция R2,1 приложена в точке А и равна по величине
реакции R1,2,
но противоположна ей по направлению.
Прикладываем уравновешивающую силу
перпендикулярно звену ОА в точке А.
,
в соответствующих точках прикладываем
все активные силы: силы тяжести, силы
инерции, моменты сил инерции и реакцию
опоры R2,1.
Также прикладываем реакцию R0,1,
которую требуется определить. Реакция R2,1 приложена в точке А и равна по величине
реакции R1,2,
но противоположна ей по направлению.
Прикладываем уравновешивающую силу
перпендикулярно звену ОА в точке А.
Определяем плечи действия этих сил:
 м.
м.
м.
Составляем уравнения моментов всех сил действующих на 1 звено относительно точки О:
;
;
Н.
Остальные силы момента относительно точки О момента не создают, т.к. действуют в той же плоскости, в которой находится само звено.
Составляем векторное уравнение равновесия всех сил, действующих на ведущее звено:
В
выбранном масштабе сил 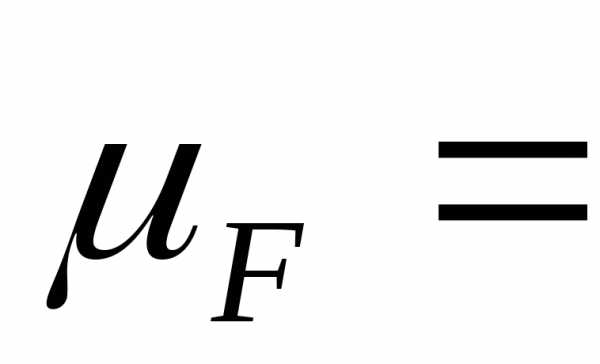 строим план сил.
строим план сил.
Рычаг Н.Е. Жуковского.
Условная уравновешивающая сила определяется методом рычага Жуковского. Для того чтобы построить рычаг Жуковского, поворачиваем план скоростей в любую сторону на 90 и параллельно перенося, наносим все активные силы, действующие на механизм в соответствующих точках. При переносе моментов сил инерции, определяем их величину для плана скоростей из отношений:
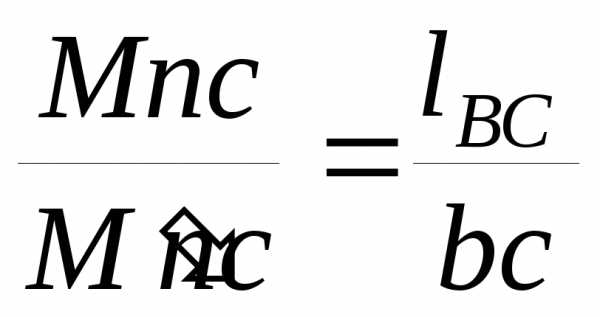 ,
,
Где:
ab, оb, cb – масштабные отрезки на плане скоростей, мм;
– длины звеньев, м.
Нмм;
Нмм;
 Нмм.
Нмм.
Плечи действия сил на рычаге Жуковского:
Н1=6 мм; Н2=26 мм; Н3=31 мм; Н4=16 мм; Н5=24 мм; Н6=39 мм; Н7=51 мм;
Составляем уравнения равновесия в форме моментов сил относительно полюса плана скоростей и определяем условную уравновешивающую силу РУр:
.
 .
.
Погрешность незначительна, на основании чего можно сделать вывод, что расчеты произведены, верно. За расчетное значение уравновешивающей силы принимаем большее из полученных значений.
Артоболевский И.И. Теория механизмов и машин: Учеб. для втузов.– 4-е изд., перераб. И доп.–М.: Наука. Гл. ред. физ-мат. лит., 1988. – 640 с..
А.С. Кореняко, Л.И. Кременштейн. Курсовое проектирование по теории механизмов и механике машин: Учеб. пособие для студентов технических вузов/Под ред. А.С. Кореняко, 5-е изд., перераб. – Киев: «Вища шк».,1970, 332с.
С.А. Попов, Г.А. Тимофеев. Курсовое проектирование по теории механизмов и механике машин: Учебое пособие для втузов/Под ред. К.В. Фролова.–3-е изд., стер. – М.: Высш. шк.,1999.
10

studfile.net
Метод планов скоростей и ускорений
Метод планов скоростей и ускорений относится к графо-аналитическим методам исследования кинематики механизмов.
Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.
Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное — движение данной точки относительно той, движение которой принято за переносное:
Этот принцип в равной степени относится к перемещениям, скоростям и ускорениям:
Планы скоростей и ускорений обладают следующими свойствами:
- на плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана. На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает;
- отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек. Вектор относительной скорости направлен на плане к той точке, которая в индексе скорости стоит на первом месте;
- фигуры, образованные точками одного и того же жесткого звена на плане и на механизме, подобны. Поэтому, если на звене известны скорости и ускорения двух точек, то скорость и ускорение любой третьей точки этого же звена можно найти по подобию;
- имея план скоростей, можно найти угловую скорость любого звена механизма. Для определения угловой скорости исследуемого звена надо взять относительную скорость двух любых точек данного звена и разделить на расстояние между этими точками на механизме;
- имея план ускорений, можно найти угловое ускорение любого звена механизма. Для определения углового ускорения исследуемого звена надо взять тангенциальную составляющую относительного ускорения двух любых точек данного звена и разделить на расстояние между этими точками на механизме;
- звенья, соединенные в поступательную кинематическую пару, имеют одинаковые угловые скорости и одинаковые угловые ускорения.
При кинематическом исследовании плоских механизмов методом планов скоростей и ускорений встречается два случая:
1) две точки (одна исследуемая, вторая с известным законом движения, которое принимается в качестве переносного) принадлежат одному и тому же жесткому звену (рисунок 13).
В данном случае относительное движение этих точек получается за счет вращательного движения звена, на котором они находятся. При определении ускорений относительное ускорение раскладывается на нормальное (известное из физики как центростремительное – стремящееся к центру вращения) и тангенциальное.
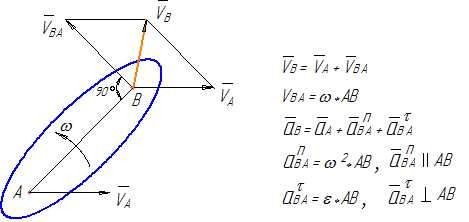
Рисунок 13
Для примера, приведенного на рисунке 13, нормальное ускорение точки В относительно точки А будет направлено вдоль радиуса ВА к точке А. Тангенциальное – перпендикулярно этому радиусу;
2) звенья соединяются поступательной парой. В этом случае рассматриваются две точки, совпадающие в данный момент времени по своему положению, но принадлежащие разным звеньям – одна ползуну, другая направляющей (рисунок 14).
Рисунок 14
Если известен закон движения направляющей 1, то известны характеристики движения любой точки на этом звене, в том числе и точки С1, принадлежащей этой направляющей.
Движение точки С1 принимается в качестве переносного. Движение точки С2, принадлежащей ползуну, относительно точки С1 получается за счет поступательного движения ползуна вдоль направляющей (влияние вращательного движения исключается, т.к. радиус вращения равен нулю – положение точек С1 и С2 совпадает). При определении ускорений кроме относительного ускорения, направленного вдоль направляющей, возникает кориолисово ускорение (см. рисунок 14).
Исследование кинематики механизма методом планов начинается с начального механизма (с входного звена) и далее ведется по группам Ассура в порядке их присоединения к механизму. Для каждой группы Ассура разработаны методы решения (уравнения и порядок построения планов), которые являются неизменными, независимо от того, в каком механизме данная группа Ассура находится.
Уравнения планов для групп Ассура второго класса приведены в таблице 3.1.
Таблица 3.1 – Кинематический анализ групп Ассура II класса методом планов
Аналитический метод кинематического исследования >
Курсовой проект по ТММ >
isopromat.ru
план скоростей и ускорений
Задача 2 Структурный и кинематический анализ механизма
Структурный анализ механизма.
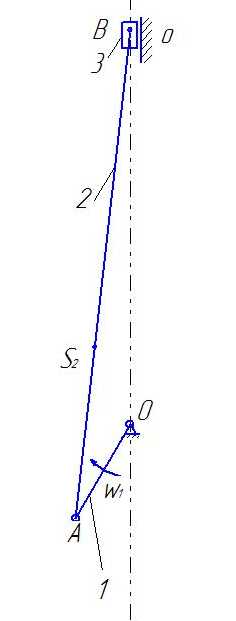
Рисунок 1 – Кинематическая схема рычажного механизма.
Число степеней свободы плоского механизма определяется по формуле П.Л. Чебышева:
,
где 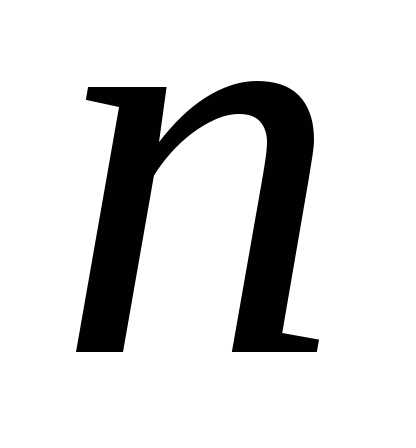 – число подвижных звеньев, n=3;
– число подвижных звеньев, n=3; 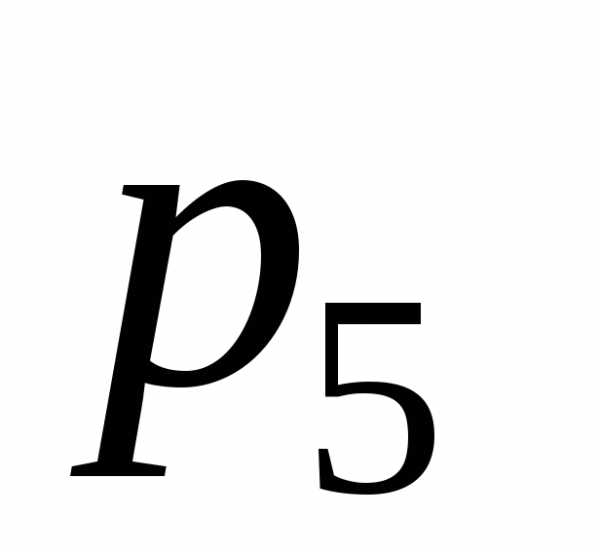 –
число кинематических пар пятого класса,
–
число кинематических пар пятого класса, 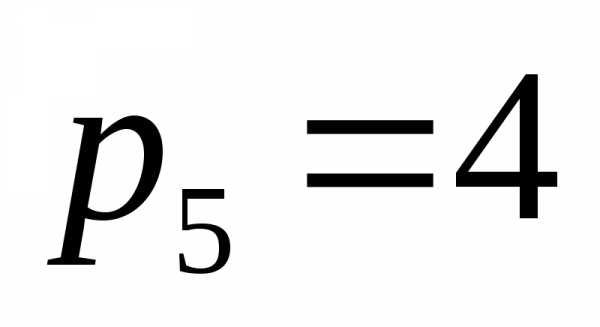 ;
; 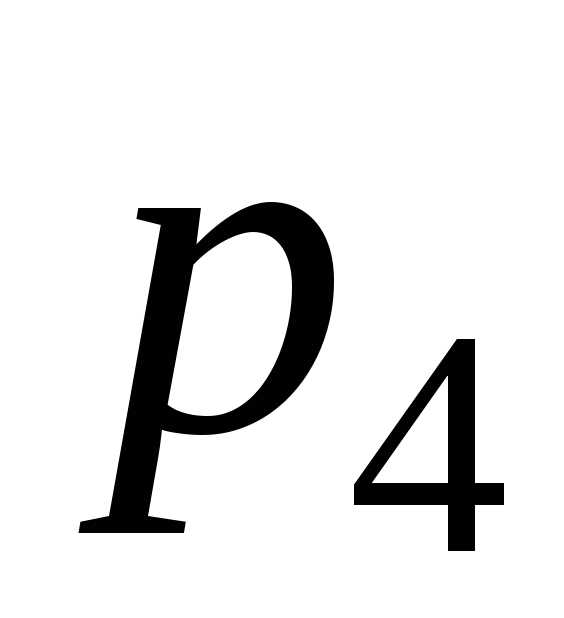 –
число кинематических пар четвертого
класса,
–
число кинематических пар четвертого
класса, 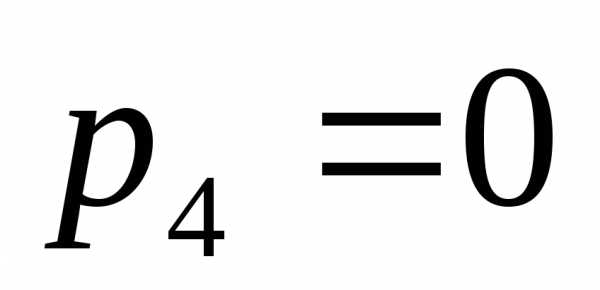 0.
0.
.
Таблица 1 – Классификация звеньев механизма
№ на КС | Название | Условное обозначение | Движение |
0 | Стойка | а) б) | Нет |
1 | Кривошип | Вращательное | |
2 | Шатун | Сложное | |
3 | Ползун | Поступательное |
Таблица 2 – Классификация кинематических пар
№ пп | Название | Условное обозначение | Элемент пары (высшая, низшая) | Класс пары |
1 | Вращательная | Поверхность, низшая | 5 | |
2 | Вращательная | Поверхность, низшая | 5 | |
3 | Вращательная | Поверхность, низшая | 5 | |
4 | Поступательная | Поверхность, низшая | 5 |
Кинематический анализ
Исходные данные: φ=1200, ω1=180 рад/с , l1= 0,0575 м, l2=0,26 м, AS2 = 0,091
Решение:
Масштаб построения кинематической схемы:
где l1 – заданная длина звена 1; (OА) – длина звена на схеме.
Строим схему механизма в заданном положении φ=1200, принимая за начало отсчета крайнее верхнее (в.м.т.) положение поршня 3 (начало рабочего хода) .
Входное (ведущее) звено 1 совершает вращательное движение c постоянной угловой скоростью .
Модуль скорости точки А определяется по формуле:
.
Построение плана скоростей
На поле чертежа произвольно выбирается
точка 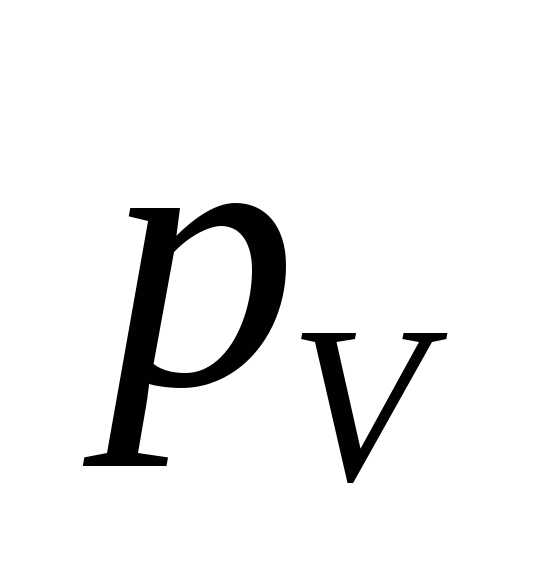 — полюс плана скоростей. Из точки
— полюс плана скоростей. Из точки  откладываем отрезок перпендикулярный OА и направленный в сторону вращения
кривошипа 1. Точка О звена OА неподвижна и находится в полюсе
откладываем отрезок перпендикулярный OА и направленный в сторону вращения
кривошипа 1. Точка О звена OА неподвижна и находится в полюсе 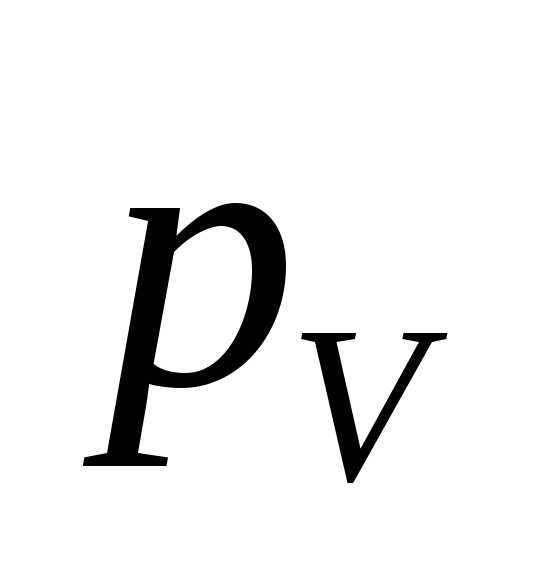 плана скоростей.
плана скоростей.
Масштаб плана скорости определяется как
.
В плоскопараллельном движении скорость точки В определяется из системы уравнений:

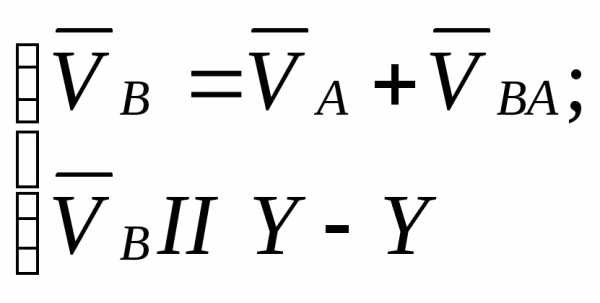
Относительная скорость 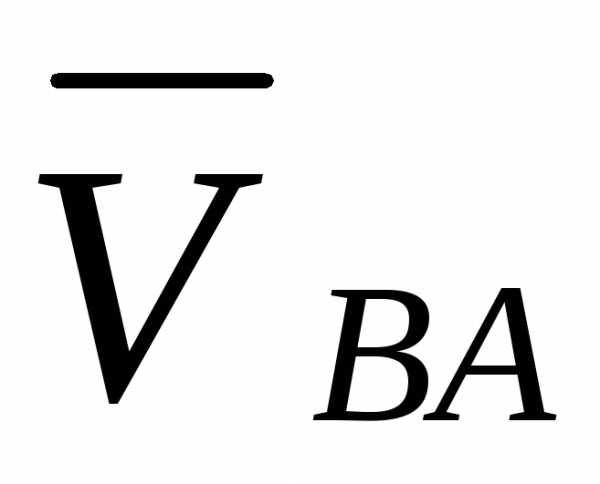 направлена перпендикулярно звену АВ.
Вектор скорости ползуна В направлен
параллельно оси Y..
направлена перпендикулярно звену АВ.
Вектор скорости ползуна В направлен
параллельно оси Y..
Положение точки S2 определяется на основании свойств подобия:
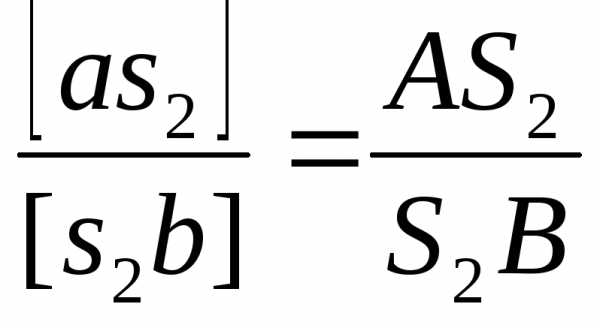 ,
откуда
,
откуда 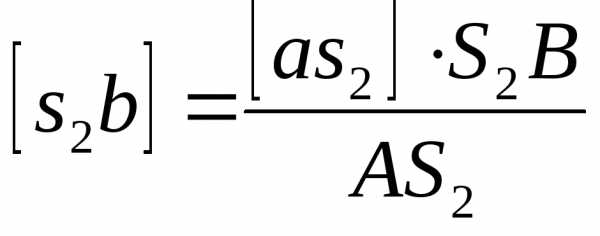 .
.
Из построенного плана скоростей определяем скорости точек и звеньев механизма
;
Угловая скорость звена 2 :
Построение плана ускорений
Построение плана ускорений производится в следующей последовательности. Ускорение точки A определится из следующего уравнения:
Нормальное ускорение точки A 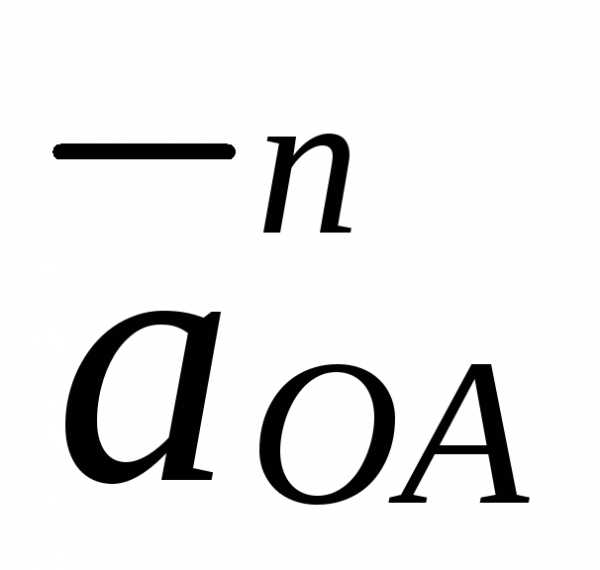 направлено по звену OA к
центру вращения , а его модуль определится
по формуле:
направлено по звену OA к
центру вращения , а его модуль определится
по формуле:
Ведущее звено 1 вращается с постоянной
угловой скоростью  ,
тогда его угловое ускорение
,
тогда его угловое ускорение  равно нулю. Тангенциальное ускорение
точки A определяется по
формуле
,
и также равно нулю.
равно нулю. Тангенциальное ускорение
точки A определяется по
формуле
,
и также равно нулю.
На поле чертежа произвольно выбирается
точка  — полюс плана ускорений. Из точки
— полюс плана ускорений. Из точки  откладывается произвольной длины
отрезок
откладывается произвольной длины
отрезок  в мм (принимаем
)
параллельно OA и направленный
от точки A к точке O.
Точка 0 звена ОА неподвижна и будет
находиться в полюсе
в мм (принимаем
)
параллельно OA и направленный
от точки A к точке O.
Точка 0 звена ОА неподвижна и будет
находиться в полюсе  плана.
плана.
Масштаб плана ускорения определяется как
В плоскопараллельном движении ускорение точки B определяется из системы уравнений:

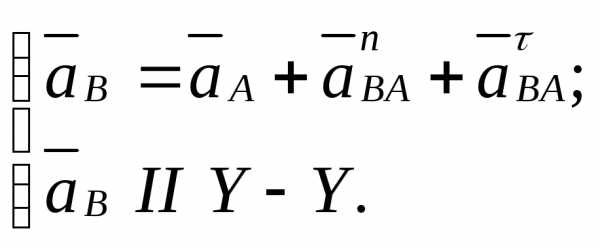
Нормальное ускорение 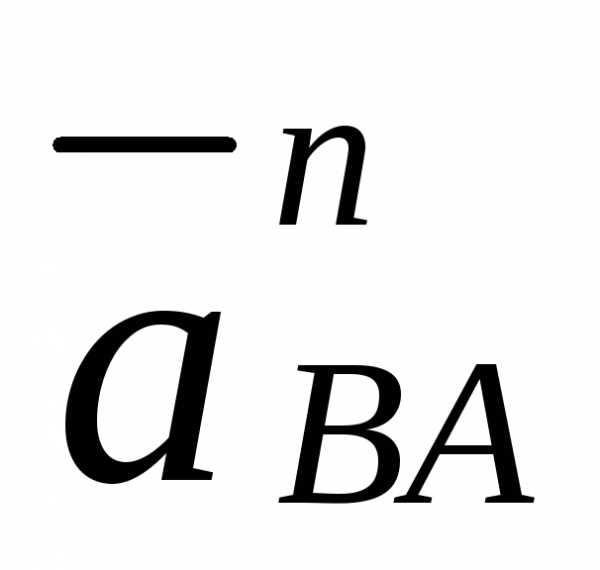 направлено параллельно звену 2 , а
тангенциальное ускорение
направлено параллельно звену 2 , а
тангенциальное ускорение 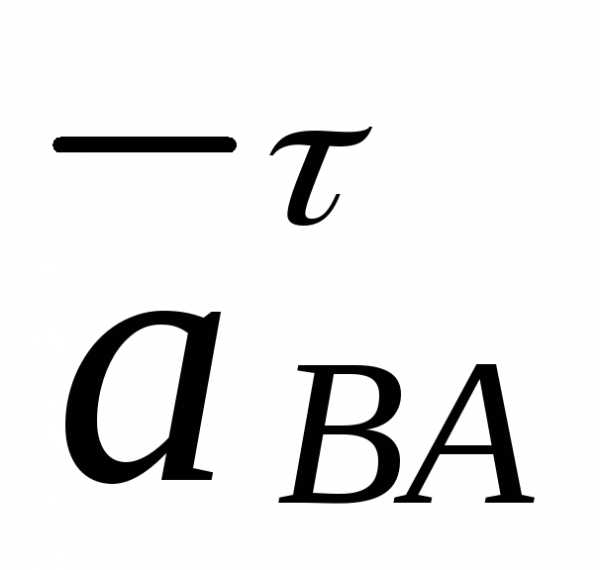 — перпендикулярно звену 2. Модуль
нормального ускорения определяем по
формуле:
— перпендикулярно звену 2. Модуль
нормального ускорения определяем по
формуле:
Длина отрезка нормального ускорения звена 2 на плане ускорений
Из плана ускорений c учетом масштаба ускорений определяем ускорения точек и звеньев механизма:
Угловое ускорение звена 2 :
Угловое ускорение направлено в соответствии с касательным ускорением.
Список литературы
1.Артоболевский И.И. Теория механизмов и машин. М.: Наука, 1988. – 640 с.
studfile.net
Методические указания по выполнению контрольной работы, страница 2
Кинематическая схема механизма предназначена для определения положений, траекторий, скоростей и ускорений точек и звеньев механизма. Для построения кинематических схем используются условные обозначения согласно ГОСТ 2770 – 68.
Планы положений механизма строятся методом засечек в масштабе (рис.2). В отличие от масштабов, применяемых в машиностроении, в теории механизмов и машин масштабы представляют собой именованные числа. Масштабы обозначаются буквой К с соответствующим индексом:
Масштабы длин и пути , м /мм;
Масштаб скоростей , м/с.мм;
Масштаб ускорений , м/с2.мм.
Численное значение масштаба должно быть либо десятичной дробью, либо целым числом и включать в себя стандартные цифры или комбинации цифр: 1, 2, 4, 5, 15, 25, 75, 10, 20…….
Для выполнения кинематического анализа данного механизма в задаче № 1 требуется вычертить в выбранном масштабе Кs положение механизма изображенное в задании и для него построить план скоростей и ускорений
1.2.2. Построение планов скоростей и ускорений
Метод построения планов скоростей и ускорений основан на теореме о разложении движения, согласно которой любое движение можно представить как сумму двух простых движений – переносного /поступательного/ и относительного /вращательного/. Тогда для скоростей:
для ускорений:
,
где — нормальная составляющая ускорения в относительном движении /определяется по данным плана скоростей/, на плане ускорений всегда направлена вдоль звена к центру относительного движения;
— касательная составляющая /определяется графически/ на плане ускорений, всегда направлена перпендикулярно к звену /радиусу/ относительного движения.
Для определения скорости или ускорения точки графическим путем не-обходимо составить систему из двух векторных уравнений. При составлении векторных уравнений движение точки рассматривается относительно двух других точек, с которыми эта точка связана и скорости которых уже известны.
Пример:
Построить план скоростей и план ускорений для заданного положения механизма, изображенного на рисунке 2.
Пусть заданы размеры звеньев механизма: ОА = 150мм; АВ = 450мм и т.д. и частота вращения входного звена / кривошипа/ОА/, соответствующая n = 200 об/мин.
План скоростей рис.3.
Скорость пальца кривошипа /точка А/ определяется по формуле:
,
где n — частота вращения кривошипа, об/мин;
ОА – длина кривошипа, м;
Подставляя данные в формулу, получим:
Задаваясь длиной отрезка /мм/, изображающего на плане скоростей вектор скорости точки А, получим масштаб плана :
Отрезок :
= 62,8 мм
выбран так, чтобы был получен стандартный масштаб скоростей.
Рекомендуется выбирать отрезок не менее 50мм.
Из полюса плата скоростей р отложим вектор скорости точки А перпендикулярно звену ОА/ по касательной к траектории движения точки А/ в сторону ее движения.
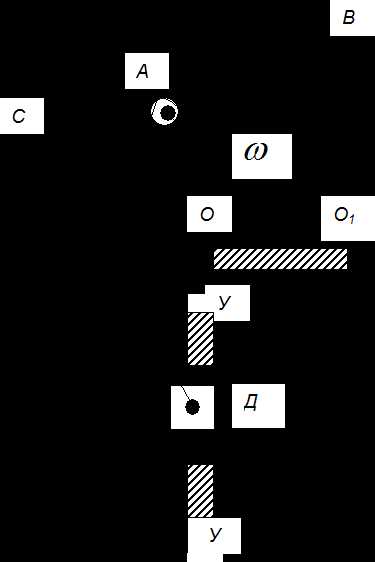
Рис.2. План механизма
КS=………………м/мм
.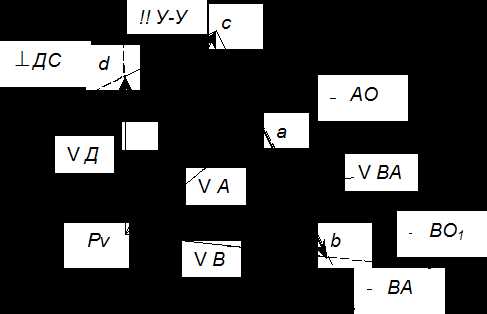
Рис.3. План скоростей
КV…………………….м/с*мм
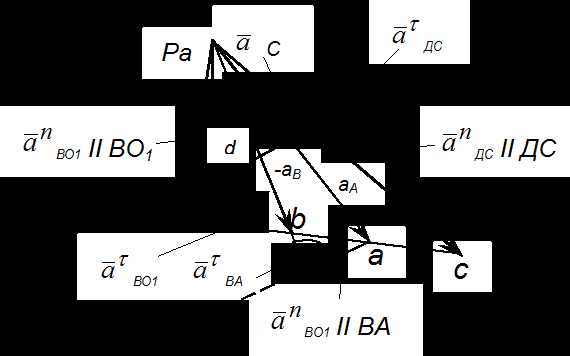 Рис.4. План ускорений
Рис.4. План ускорений
Кa……………………………м/с2мм
Рассматривая движение точки В относительно точки А, а затем относительно ОI, имеем:
Из конца вектора скорости /точка а/ проводим линию действия вектора относительной скорости перпендикулярно звену АВ, а затем из полюса p /т.к. V0 = 0/ перпендикулярно звену ВОI проводим линию действия вектора относительной скорости до пересечения с линией действия вектора в точке в. Отрезокизображает вектор абсолютной скорости точки В .
Скорость точки С /третьей точки звена ВАС/ найдем методом подобия. Можно записать следующее соотношение:
или ,
где и — отрезки на плане скоростей;
АС и АВ – размеры звеньев механизма.
Вычислив отрезок и отложив его на плане скоростей, получим точку . Соединяя точку с полюсом , найдем отрезок , изображающий вектор абсолютной скорости точки С (Vc).
Для определения скорости точки Д рассмотрим движение этой точки относительно точек С и Ду / точка Ду принадлежит неподвижным направляющим и в данный момент совпадает с точкой Д /.
Система векторных уравнений имеет вид:
Так как VДУ =0, то .
Из конца вектора скорости точка с / проводим линию действия вектора относительной скорости перпендикулярно звену СД, а из полюса p параллельно оси у-у проводим линию действия вектора относительной скорости в точке d . Отрезок изображает вектор абсолютной скорости точки Д .
Абсолютные скорости каждой точки равны:
VВ = , м/с
VС = , м/с
VД = , м/с
Относительные скорости:
VВА =
=
VДС =
План ускорений рис.4.
Рассматривая движение точки А относительно точки О, можно записать:
Ускорение ао = 0, т.к. сonst. Следовательно, точка А при постоянной угловой скорости кривошипа будет иметь только нормальное / центральное/ ускорение:
Величина нормального ускорения:
Подставляя числовые значения, получим:
Задаваясь длиной отрезка изображаемого на плане ускорений вектор ускорения точки А, получим масштаб плана ускорений
Отрезок выбран равным 65,8 мм, чтобы получить стандартный масштаб ускорений.
Из полюса плана ускорений откладываем вектор ускорения точки А
/отрезок / параллельно звену АО, направляя его от точки А к центру ее вращения – точке О.
Рассматривая движение точки В относительно точки А, а затем относительно точки О1, имеем:
Так как то .
Нормальное ускорение В в ее относительном движении относительно точки А по величине определяется следующим образом:
Удобнее сразу находить величину отрезка, изображаемого вектор нормального ускорения:
где — отрезок, изображений вектор относительной скорости на плане скоростей, мм;
АВ – длина шатуна, м.
Направлен вектор по шатуну от точки В к точке А.
Вектор касательного ускорения известен только по направлению – линия его действия перпендикулярна звену ВА.
Нормальное ускорение:
vunivere.ru
Построение плана положений
План положений механизма строится по заданным размерам методом засечек в положении, определяемом углом начального звена, в масштабе.
Длина отрезка (в миллиметрах), изображающая на плане начальное звено, берется произвольно. Рекомендуется принимать ее кратной реальной длине звена. Размеры остальных звеньев находятся с учетом выбранного масштаба длин. Например, если реальная длина звена составляет 0.5 м., то на плане положений ее рекомендуется выполнять длиной 50, 100 или 150 мм, исходя из удобства построений. Таким образом, масштабный коэффициент ( 2 .5) составит: 0.01, 0.005, 0.0025 соответственно. Условные обозначения кинематических пар и звеньев, загромождающих чертеж и затрудняющих его восприятие, допускается не выполнять.
Построение планов скоростей и ускорений
Абсолютное движение точек звеньев (относительно стойки) раскладывается на переносное и относительное движения и равно их векторной сумме. Переносное движение должно быть известно. Под ним понимается движение точки звена с известной скоростью или ускорением.
В качестве центров переноса выбираются, как правило, центры шарниров. Поэтому движение центров шарниров определяется в первую очередь. Если линия действия абсолютного движения неизвестна, то при его разложении используются 2 центра переноса.
Таким образом, вектор абсолютной скорости определяется выражением:
( 2.6)
где вектор переносной скорости;
вектор относительной скорости.
Вектор абсолютного ускорения выражается:
( 2.7)
где вектор переносного ускорения;
вектор относительного ускорения.
Вектор относительного ускорения , в общем случае, раскладывается на нормальное ускорение, касательное ускорениеи ускорение Кориолиса:
( 2.8)
Кинематический анализ механизма начинается с исследования кинематики первичного механизма и ведется по группам Ассура в порядке их наслоения.
После построения измеряются длины векторов скоростей и ускорений, определённых в ходе анализа. Величины скоростей и ускорений находятся как произведение длины вектора, изображающего соответствующую величину (скорость или ускорение) на плане на масштабный коэффициент плана.
Кинематический анализ кривошипно-коромыслового механизма.
Кривошипно-коромысловый механизм состоит из первичного механизма и группы Ассура ВВВ (рисунок )
а)б)
Рисунок 2.4 — Первичный механизм (а) и группа Ассура ВВВ (б).
Общая методика построения плана положений:
Произвольно, исходя из удобства построений, построить первичный механизм (кривошип ОА) в положении 0 ( рисунок 2 .5).
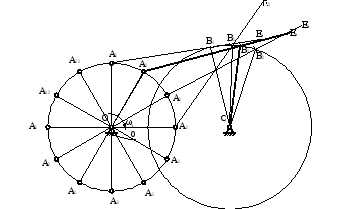
Рисунок 2.5 — Планы положений кривошипно–коромыслового механизма.
Определить масштабный коэффициент. Формула 2 .5 для определения масштабного коэффициента преобразуется к виду:
, , ( 2.9)
где − масштабный коэффициент плана положений;
OA– реальный размер звенаOA;
− длина отрезка, изображающего звеноOAна плане положений.
Все дальнейшие построения проводятся с учетом масштабного коэффициента.
Провести окружность радиусом ОА, которая представляет собой траекторию движения точки А относительно стойки.
Нанести на план точку С.
Построить траекторию движения точки В относительно стойки − окружность радиуса ВС.
Из точки А0построить дугу окружности радиусом АВ до пересечения с траекторией движения точки В относительно стойки.
Место пересечения обозначить В0.
Точку А0соединить с точкой В0.
Полученный отрезок А0В0продлить на расстояние ВЕ и нанести точку Е0.
Таким образом, получаем план положений механизма для положения 0. Для остальных положений повторяем вышеописанные действия. На рисунке 2 .5 показаны планы для четырех положений механизма. План положения 1 выделен утолщенной линией.
Общая методика построения плана скоростей:
Произвольно, исходя из удобства размещения на чертеже, выбрать положение полюса плана скоростей (рисунок 2 .6).
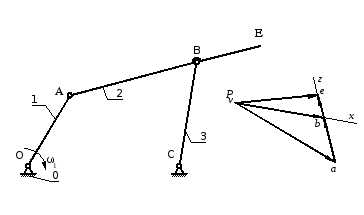
Рисунок 2.6 — План скоростей кривошипно–коромыслового механизма.
Определить величину линейной скорости точки Аведущего звена механизма (кривошипа) из выражения
( 2.10)
Направление линейной скорости точки перпендикулярнои совпадает с направлением угловой скорости.
Из полюса построить отрезок, изображающий вектор абсолютной скорости точкиперпендикулярнопо направлению угловой скорости(рисунок 2 .6). Длина отрезка выбирается произвольно, исходя из удобства построений. При этом масштаб плана скоростей определяется по формуле:
, .( 2.11)
Составить векторные уравнения для определения вектора абсолютной скорости точки В. Движение точкиВявляется сложным, поэтому рассмотрим движение точкиВвокруг двух центров переноса. Относительно первого вместе с шатуном 2 , в качестве центра переноса выбираем точкуА, скорость которой известна. Относительно второго центра переноса вместе с коромыслом3. В качестве центра переноса выбираем точкуС, вектор скорости которой тоже известен. Система векторных уравнений имеет вид:
где вектор скорости точкиВотносительно полюса переносаА–относительное движение (линия его действия известна, она перпендикулярноВА).
вектор скорости точкиВотносительно полюса переносаС(линия его действия известна, она перпендикулярнаВС).
Через конец отрезка , изображающего вектор абсолютной скорости точки, провести линию действияперпендикулярно звену АВ (отрезокрисунок 2 .6). Через конец вектора скоростиС(т.к.то через полюс) провести линию действияперпендикулярно звену ВС (отрезок). На пересечении этих линий получается конец отрезка, изображающего вектор скорости точкиВ. Полученный отрезокизображает вектор абсолютной скороститочкиВ.
Построить вектор абсолютной скорости точки E, используя метод подобия фигур на схеме механизма и плане скоростей. Соответствующее соотношение выглядит следующим образом:
( 2.12)
На отрезке плана скоростей отложим отрезок(рисунок 2 .6). Соединив полюсс точкой, получим отрезок, изображающий вектор абсолютной скорости точкиE.
Определить модули искомых скоростей. Отрезки, изображающие векторы скоростей и,измерить на плане скоростей и умножить на масштаб плана скоростей:
;
;( 2.13)
.
Определить абсолютные угловые скорости звеньев. Это скорости вращения звеньев относительно стойки. Значения этих скоростей определяются по выражениям:
где , ,– длины звеньев реального механизма.
Направления абсолютных угловых скоростей определяются по направлениям векторов соответствующих относительных линейных скоростей.
Общая методика построения плана ускорений:
Выбрать положение полюса плана ускорений (рисунок 2 .7). В полюсе берут начало векторы абсолютных ускорений точек механизма.
Рисунок 2.7 — План ускорений кривошипно–коромыслового механизма.
Из полюса построить отрезок, изображающий вектор ускорения точки А. Так как угловая скоростьпостоянна, то касательное ускорение точки А равно нулю. Следовательно вектор ускоренияравен вектору нормального ускорения точки А (параллелен ОА и направлен к центру вращения). Величина ускорения точки А определяется из выражения:
. ( 2.14)
Длина отрезка выбирается из тех же соображений, что и длина отрезкана плане скоростей. При этом масштаб плана ускорений определяется по формуле:
,. ( 2.15)
Составить векторные уравнения для определения абсолютного ускорения точки В. Векторные уравнения имеют вид:
где вектора нормального и касательного ускорений точкиВотносительно центра переносаА.
вектора нормального и касательного ускорений точкиВотносительно центра переносаС.
Определить величину ускорения из выражения:
. ( 2.16)
На плане ускорений из конца отрезка, изображающего вектор ускорения , провести отрезок, изображающий вектор ускорения. Направление вектора —параллелен звенуABи ориентирован от точки В к точке А. Длина вектора определяется из выражения:
. ( 2.17)
На плане ускорений провести линию действия касательного ускорения перпендикулярноAB(линия 2-2).
Определить величину нормального ускорения из выражения:
. ( 2.18)
На плане ускорений построить вектор нормального ускорения . Вектор параллелен звенуBCи направлен от точки В к точке С. Ускорениеравно нулю, следовательно начало вектора находится в полюсе. Длина вектора определяется из выражения:
.( 2.19)
На плане ускорений провести линию действия касательного ускорения перпендикулярноBC(линия 1-1).
На пересечении линий 1−1 и 2−2 построить точку b. Построить вектор абсолютного ускорения точки В.
Построить вектор абсолютного ускорения точки E, используя метод подобия фигур на схеме механизма и плане ускорений. Соответствующее соотношение выглядит следующим образом:
( 2.20)
Вычислить модули ускорений точек механизма:
( 2.21)
Вычислить угловые ускорения звеньев механизма:
( 2.22)
( 2.23)
Направление угловых ускорений совпадает с направлением касательных ускорений перенесенных с плана ускорений на механизм.
studfile.net
План скоростей

3.КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКИХ МЕХАНИЗМОВ
3.3.Метод кинематических планов
геометрическую сумму вектора скорости точки С и вектора скорости относительного вращательного движения точки В вокруг условно неподвижной точки С:
VB =VС +VBС .
Линия действия вектора относительной скорости VBС является пер-
пендикуляром к оси кулисы 3 (рис. 3.5, к), а на плане скоростей этот вектор направлен к той точке, которая стоит первой в индексе при векторе этой скорости.
Вектор ускорения точки В, принадлежащей кулисе 3 (рис. 3.5, а), представляет собой геометрическую сумму вектора ускорения точки С и векторов
нормального ускорения aBnС и тангенциального ускорения aBτС :
aB = aC + aВСn + аВСτ .
Траекторией относительного вращательного движения точки В вокруг неподвижной точки С является окружность, радиус которой равен действительной длине кулисы 3 (рис. 3.5, к). Следовательно, линия действия вектора
нормального ускорения aBnС параллельна оси кулисы 3 (рис. 3.5, к), а вектор
этого ускорения направлен к центру вращения, т. е. от точки В, стоящей первой в индексе при векторе этого ускорения, к точке С, стоящей второй в этом
же индексе. Линия действия вектора тангенциального ускорения aBτС являет-
ся перпендикуляром к оси кулисы 3 (рис. 3.5, к), а вектор на плане ускорений направлен к той точке, которая стоит первой в индексе при векторе этого ускорения.
Векторы скорости и ускорения точки В, принадлежащей синусоиду 3 (рис. 3.5, л) и тангенсоиду 3 (рис. 3.5, м), действуют по линиям, параллельным прямым ВС, т. к. данные звенья 3 могут совершать только возвратно-
поступательные движения параллельно прямой ВС, т. е. VВ и aB || BC.
Планскоростей
Масштабный коэффициент плана скоростей, м/(с мм), рассчитывается по формуле
μV = VрAaО ,
Теория механизмов и машин. Учеб. пособие | -55- |

3.КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКИХ МЕХАНИЗМОВ
3.3.Метод кинематических планов
где рa – произвольный отрезок, мм.
Из определения плана скоростей вытекают его свойства:
1)все векторы, составляющие план, являются векторами скоростей характерных точек механизма;
2)все векторы скоростей, выходящие из полюса плана (точки р), являются векторами линейных скоростей характерных точек механизма;
3)все векторы скоростей, не проходящие через полюс плана (точку р), являются векторами относительных скоростей характерных точек механизма;
4)скорости характерных точек механизма, равные нулю, изображаются точечными векторами, совпадающими с полюсом плана скоростей (точкой р).
После построения плана скоростей и определения значений скоростей всех характерных точек механизма переходят к определению значений и направлений действия угловых скоростей звеньев механизма.
Угловая скорость – это отношение скорости относительного движения соответствующего звена механизма к действительной длине этого звена.
Направление действия угловой скорости звеньев, совершающих вращательные или сложные движения, указывает вектор относительной скорости характерных точек соответствующего звена, перенесенный с плана скоростей в одноименную точку, принадлежащую этому звену на схеме механизма. При этом разрывается связь рассматриваемого звена с другими звеньями, а к свободной характерной точке прикладывается шарнирнонеподвижная опора. В этом случае данная точка становится условно неподвижной, а одноименная точка совместно со звеном под действием вектора относительной скорости получает возможность совершать вращательное движение вокруг условно неподвижной точки в направлении действия этого вектора. Полученное направление вращательного движения рассматриваемого звена является направлением действия угловой скорости этого звена. Угловая скорость звеньев механизмов, совершающих поступательные движения, равна нулю.
Планускорений
План ускорений – это пучок векторов, выполненный в определенном масштабном коэффициенте, лучи которого изображают векторы абсолютных ускорений характерных точек механизма, а отрезки, соединяющие их вершины, соответствуют векторам относительных ускорений.
Масштабный коэффициент плана ускорений, м/(с2 мм), вычисляют по формуле
|
|
|
| μа = |
|
| аn |
|
| , |
|
|
|
|
|
| ОА |
|
| ||
|
| πa |
|
| ||||||
|
| |||||||||
|
|
|
|
|
|
|
|
|
| |
где |
| πa |
| – произвольный отрезок, мм. |
|
|
|
|
| |
|
|
|
|
|
|
| ||||
Теория механизмов и машин. Учеб. пособие | -56- |

3.КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКИХ МЕХАНИЗМОВ
3.3.Метод кинематических планов
Из определения плана ускорений вытекают его свойства:
1)все векторы, составляющие план, являются векторами ускорений характерных точек механизма;
2)все векторы ускорений, выходящие из полюса плана (точки π), являются векторами абсолютных ускорений характерных точек механизма;
3)все векторы ускорений, не проходящие через полюс плана (точку π), являются векторами относительных ускорений характерных точек механизма;
4)ускорения характерных точек механизма, равные нулю, изображаются
точечными векторами, совпадающими с полюсом плана ускорений (точкой π). Следствие из свойства 4. Если тангенциальные или радиальные ускорения характерных точек механизма равны нулю, то они изображаются точечными векторами, совпадающими на плане ускорений с вершинами векто-
ров (нормальных или Кориолисова) ускорений этих же точек механизма. После построения плана ускорений и определения значений ускорений
всех характерных точек механизма переходят к определению значений и направлений действия угловых ускорений звеньев механизма.
Угловое ускорение – это отношение тангенциального (касательного) ускорения звена механизма к действительной длине этого звена.
Направление действия углового ускорения звеньев, совершающих вращательные или сложные движения, указывает вектор тангенциального ускорения характерных точек соответствующего звена, перенесенный с плана ускорений в одноименную точку, принадлежащую этому звену на схеме механизма. При этом разрывается связь рассматриваемого звена с другими звеньями, а к свободной характерной точке прикладывается шар- нирно-неподвижная опора. В этом случае данная точка становится условно неподвижной, а одноименная точка совместно со звеном под действием вектора тангенциального ускорения получает возможность совершать вращательное движение вокруг условно неподвижной точки в направлении действия этого вектора. Полученное направление вращательного движения рассматриваемого звена является направлением действия углового ускорения этого звена. Угловое ускорение звеньев механизмов, совершающих поступательные движения, равно нулю.
Теоремаподобия
Модели плоских рычажных механизмов могут содержать характерные точки, являющиеся центрами кинематических пар, которые образованы звеньями, не имеющими связей с элементами стойки. Определение скоростей и ускорений подобных точек осуществляется по теореме подобия, которая формулируется следующим образом: отрезки, соединяющие точки на схеме (плане положений) механизма, и отрезки, соединяющие одноименные точки на планах скоростей или ускорений, образуют подобные фигуры.
Теория механизмов и машин. Учеб. пособие | -57- |

3.КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКИХ МЕХАНИЗМОВ
3.3.Метод кинематических планов
Если порядок букв при обходе по контуру в выбранном направлении одинаков, то подобные фигуры к тому же и сходственно расположены. Фигура, полученная на плане ускорений, будет повернута относительно исходной фигуры схемы (плана положений) механизма на некоторый угол в направлении вращения ведущего звена.
Согласно формулировке теоремы подобия, характерная точка, являющаяся центром кинематической пары, образованной звеньями механизма, не имеющими связей со стойкой, лежит на схеме механизма на некотором звене, следовательно, одноименная точка как на плане скоростей, так и на плане ускорений расположена на отрезке, изображающем это звено в составе обоих планов. Составив пропорцию, характеризующую отношение действительных длин звеньев и отрезков, соответствующих этим параметрам в составе планов, найдем длину отрезка, определяющего положение рассматриваемой точки как на плане скоростей, так и на плане ускорений. Отложив длину полученного отрезка на планах скоростей и ускорений, установим положение искомой точки. Соединив найденные точки с полюсами планов, получим отрезки, пропорциональные, соответственно, векторам скорости и ускорения рассматриваемой характерной точки. Полученные векторы скорости и ускорения будут направлены от полюсов планов к найденным точкам. Значение скорости и ускорения рассматриваемой характерной точки рассчитаем как произведение длины отрезка с соответствующего плана на его масштабный коэффициент.
Теория механизмов и машин. Учеб. пособие | -58- |
studfile.net
