Треугольник 3 4 5 – Египетский треугольник | Любопытные подробности обо всем на свете! — novokazan.ru

Содержание

Египетский треугольник — загадка древности :: SYL.ru

Известный математик Пифагор совершил множество различных открытий, но большинству людей, которым не приходится регулярно сталкиваться с алгеброй и геометрией, он известен благодаря своей теореме. Ученый открыл ее, пребывая в Египте, где его очаровала красота и изящность пирамид, а это, в свою очередь, натолкнуло его на мысль о том, что в их формах прослеживается определенная закономерность.

История открытия

Своим названием египетский треугольник обязан эллинам, которые часто посещали Египет в VII-V веках до н. э., среди них был и Пифагор. Основой пирамиды Хеопса является прямоугольный многоугольник, а

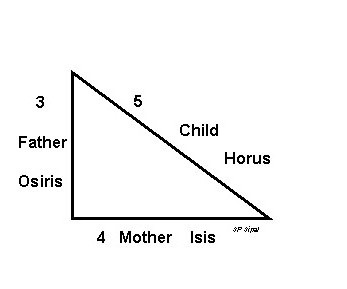
пирамиды Хефрена – так называемый египетский треугольник, который древние называли священным. Плутарх писал, что жители Египта соотносили природу с этой геометрической фигурой: вертикальный катет символизировал мужчину, основание – женщину, а гипотенуза – ребенка. Соотношение сторон в нем равно 3:4:5, а это приводит к теореме Пифагора, так как 3²х 4²= 5². Следовательно, тот факт, что в основании пирамиды Хефрена лежит египетский треугольник, позволяет утверждать, что знаменитая теорема была известна жителям древнего мира еще до того, как ее сформулировал Пифагор. Особенностью этой фигуры также считается то, что благодаря такому соотношению сторон она является первым и простейшим из Героновых треугольников, поскольку ее стороны и площадь целочисленные.

Применение

Египетский треугольник с древности пользовался популярностью в архитектуре и строительстве.

В основном он использовался тогда, когда строили прямые углы с помощью шнура или веревки, разделенной на 12 частей. По отметкам на такой веревке можно было очень точно создать прямоугольную фигуру, катеты которой будут служить направляющими для установки прямого угла строения. Известно, что такие свойства этой геометрической фигуры использовались не только в Древнем Египте, но и, задолго до этого, в Китае, Вавилоне и Месопотамии. Для создания пропорциональных сооружений в Средние века также использовался египетский треугольник.

Углы

Соотношение сторон этого треугольника 3:4:5 приводит к тому, что он является прямоугольным, т. е. один угол равен 90 градусам, а два других – 53,13 и 36,87 градусам. Прямым является угол между сторонами, соотношение которых равно 3:4.

Доказательство

При помощи некоторых простых вычислений можно доказать, что треугольник является прямоугольным. Если следовать теореме обратной той, которую создал Пифагор, т. е. в случае, если сумма квадратов двух сторон будет равняться квадрату третьей, то он прямоугольный, а поскольку его стороны приводят к равенству 3²х 4²= 5², следовательно, он является прямоугольным.
Подводя итог, надо отметить, что египетский треугольник, свойства которого уже в течение многих столетий известны человечеству, на сегодняшний день продолжает использоваться в архитектуре. Это вовсе неудивительно, ведь такой способ гарантирует точность, которая очень важна при строительстве. Кроме этого, он очень прост в использовании, что тоже значительно облегчает процесс. Все преимущества использования этого метода прошли проверку веками и остаются популярными до сих пор.

www.syl.ru

Планиметрия. Страница 5


	Главная > Учебные материалы > Математика: Планиметрия. Страница 5


	1.Теорема Пифагора. 2.Египетский треугольник. 3.Соотношение между углами и сторонами в прямоугольном треугольнике. 4.Основные тригонометрические тождества. 5.Примеры.
1 2 3 4 5 6 7 8 9 10 11 12


	1.Теорема Пифагора
	Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Доказательство. 1. Разделим каждую сторону большого квадрата на два отрезка x и y точкой. И проведем через эти точки отрезки. 2. Тогда треугольники 1,2,3,4 равны по двум сторонам и углу между ними. 3. Т.к. сумма углов α + β = 90°, то фигура внутри большого квадрата тоже квадрат. (Все стороны = с и все углы = 90° ) 4. Площадь большого квадрата равна сумме площадей малого квадрата и 4-х треугольников. (Рис.1)	Рис.1 Теорема Пифагора.


	2.Египетский треугольник

	Пусть дан треугольник со сторонами АВ = a, ВС = b, АС = c. При условии, что а² + b² = с². Доказать, что угол, лежащий против стороны с, прямой. Допустим, что треугольник АВС не прямоугольный. Тогда можно опустить высоту на сторону АС — h (Рис.2). Из двух прямоугольных треугольников ABD и DBC составим следующую систему уравнений по теореме Пифагора. Обозначим AD как х, BD — высота h. Но по условию задачи а² + b² = с². Следовательно х = 0 и сторона а = h. Т.е. угол между сторонами АВ и АС — прямой. В древнем Египте данное соотношение применялось очень широко. Например для построения прямого угла между сторонами при строительстве зданий и сооружений. Или при измерении прямых углов пахотных земель. Так как зная соотношение, можно легко построить прямой угол. По этой причине треугольник со сторонами 3,4,5 ед. называют Египетским треугольником.	Рис.2 Египетский треугольник.

	3.Соотношение между углами и сторонами в прямоугольном треугольнике

	Пусть дан прямоугольный треугольник АВС. Проведем прямую ЕF параллельную стороне АВ (Рис.3). Тогда по теореме о пропорциональных отрезках: Т.е. соs α не зависит от размеров прямоугольного треугольника, а зависит только от величины угла. Тогда по теореме Пифагора sin α также зависит только от величины угла. А следовательно tg α и ctg α. Отсюда можно сделать следующие выводы: AB = BC sin α AC = BC cos α AB = AC tg α AC = AB ctg α	Рис.3 Соотношение между углами и сторонами в прямоугольном треугольнике.





	4.Основные тригонометрические тождества
	Пусть дан прямоугольный треугольник со сторонами a,b,c. (Рис.4)	Рис.4 Основные тригонометрические тождества.



	5.Пример 1
	У треугольника одна сторона равна 1 м, а прилегающие к ней углы 30° и 45°. Найдите другие стороны треугольника. (рис.5)

	Так как один из углов 30 градусов, то катет, лежащий против этого угла равен половине гипотенузы, т.е. h = b/2. А следовательно КС = h, т.к. угол β = 45 градусов.	Рис.5 Задача. У треугольника одна сторона равна 1 м…

	Пример 2
	Найдите высоту равнобокой трапеции, если ее основания равны 6 м и 12 м, а боковая сторона равна 5 м. (Рис.6)

	Решение: Пусть ABCD данная трапеция. ВЕ перпендикуляр, опущенный на основание AD. Тогда АЕ = (12 — 6)/ 2 = 3 м. Так как АЕ = FD. По теореме Пифагора: АВ² = AE² + BE² Следовательно: 5² = 3² + BE² 25 = 9 + BE² BE² = 16 BE = 4 м.	Рис.6 Задача. Найдите высоту равнобокой трапеции…


	Пример 3
	Докажите, что расстояние между двумя точками на сторонах треугольника не больше большей из его сторон. (Рис.7)

	Доказательство: Пусть ABC данный треугольник. АС — его большая сторона. Проведем отрезок DE параллельно стороне АС. Необходимо доказать, что отрезок DE меньше стороны АС. Если мы докажем, что отрезок DE меньше большей стороны АС, то при взятии двух других точек треугольника на других его меньших сторонах, отрезок между этими точками будет также меньше стороны АС. Опустим перпендикуляр BF на большую сторону АС. Составим следующее соотношение: АС = АВ сos α + ВС cos β Тогда отрезок DE будет равен: DE = DB сos α + ВE cos β Так как DB то следовательно, отрезок DE меньше стороны АС. Допустим, что отрезок DE непараллелен стороне АС (рис.7 б). Тогда можно взять отрезок DE₁ параллельный АС, который больше чем DE, и доказать, что DE₁ меньше стороны АС аналогичным образом.	Рис.7 Задача. Докажите, что расстояние между двумя точками…

	Пример 4
	Докажите, что прямая, отстоящая от центра окружности на расстояние меньше радиуса, пересекает окружность в двух точках. (Рис.8)

	Доказательство: Пусть дана окружность с центром в точке О. И прямая а, отстоящая от центра окружности точки О, на расстояние ОЕ = h Обозначим прямую, на которой лежит отрезок ОЕ, как b. Пусть точка О делит прямую b на две полупрямые, одна из которых ОЕ. Согласно аксиоме, от любой полупрямой, от ее начальной точки (точки О), в заданную полуплоскость, можно отложить только один угол определенной градусной меры α. Следовательно, отрезок ОЕ = h = ОАcos α. Но так как прямая b делит плоскость на две полуплоскости, то от полупрямой ОЕ, от ее начальной точки (точки О) можно отложить такой же угол, той же градусной меры и во вторую полуплоскость, т.е. -α. Так, что ОЕ = h = ОВcos (-α). Таким образом, если выполняется условие R = OA > h, то прямая а будет иметь две точки пересечения. Так как h = ОАcos α = ОВcos (-α) Радиусы ОА и ОВ можно рассматривать как две наклонные, отложенные в двух полуплоскостях, в треугольнике АОВ перпендикуляра ОЕ.	Рис.8 Задача. Докажите, что прямая, отстоящая от центра окружности…


	Пример 5
	Даны три положительных числа a,b,c. Докажите, что если каждое из этих чисел меньше суммы двух других, то существует треугольник со сторонами a,b,c. (Рис.9)

	Доказательство: Пусть даны три точки. Если эти три точки лежат на одной прямой, например А,Е,С, то расстояния между этими точками связаны соотношением: АС = АЕ + ЕС Отсюда видно, что каждое из трех расстояний не больше двух других. Т.е. расстояние между точками А и С не больше двух расстояний АЕ и ЕС. Если взять три точки, не лежащих на одной прямой, например А,В,С и опустить перпендикуляр ВЕ, то АС так как АЕ и ЕС являются проекциями AB и ВС на сторону АС. А любая проекция наклонной всегда меньше (в крайнем случае равна) самой наклонной. Т.е. АE < AB, a EC < BC. Таким образом, концы отрезков АВ и СВ смогут совпасть в одной точке В. И можно построить треугольник. Предположим, что расстояние АС > AB + BC (Рис.9 б). Тогда концы отрезков АВ и СВ не смогут совпасть в точке В. Так как, если даже отрезки такой же длины отложить на отрезке АС, то получится, что АС > АВ + СB₁ = AE + CE₁, Таким образом, если числа a,b и с принять за длины отрезков, то концы отрезков АВ и СВ не смогут совпасть в одной точке В. Между ними образуется некое расстояние ВВ₁ и построить треугольник не получится.	Рис.9 Задача. Даны три положительных числа…







1 2 3 4 5 6 7 8 9 10 11 12

	Содержание

	Страница 1	Страница 7
	1.Основные фигуры планиметрии. 2.Аксиомы планиметрии. 3.Смежные углы. 4.Вертикальные углы. 5.Перпендикулярные прямые. 6.Признаки равенства треугольников.	1.Движение и его свойства. 2.Симметрия относительно точки. 3.Симметрия относительно прямой. 4.Параллельный перенос и его свойства.

	Страница 2	Страница 8
	1.Параллельность прямых. 2.Признаки параллельности прямых. 3.Свойство углов при пересечении параллельных прямых. 4.Сумма углов треугольника. 5.Единственность перпендикуляра к прямой. 6.Высота, биссектриса и медиана треугольника. 7.Свойство медианы равнобедренного треугольника.	1.Вектор и его абсолютная величина. 2.Сложение векторов. 3.Умножение вектора на число. 4.Разложение вектора по двум неколлинеарным векторам. 5.Скалярное произведение векторов.

	Страница 3	Страница 9
	1.Окружность. 2.Окружность описанная около треугольника. 3.Окружность вписанная в треугольник. 4.Геометрическое место точек.	1.Преобразование подобия и его свойства. 2.Подобие фигур. Подобие треугольников по двум углам. 3.Подобие треугольников по двум пропорциональным сторонам и углу между ними. 4.Подобие треугольников по трем пропорциональным сторонам. 5.Подобие прямоугольных треугольников.

	Страница 4	Страница 10
	1.Параллелограмм. 2.Свойства диагоналей параллелограмма. 3.Ромб. 4.Теорема Фалеса. 5.Средняя линия треугольника. 6.Трапеция. 7.Теорема о пропорциональных отрезках.	1.Углы, вписанные в окружность. 2.Пропорциональность хорд и секущих окружности. 3.Теорема косинусов. 4.Теорема синусов. 5.Соотношение между углами и сторонами в треугольнике.

	Страница 5	Страница 11
	1.Теорема Пифагора. 2.Египетский треугольник. 3.Соотношение между углами и сторонами в прямоугольном треугольнике. 4.Основные тригонометрические тождества.	1.Многоугольники. Правильные многоугольники. 2.Радиус вписанной и описанной окружностей правильных многоугольников. 3.Подобие многоугольников. 4.Длина окружности.

	Страница 6	Страница 12
	1.Декартова система координат. 2.Расстояние между точками. 3.Уравнение окружности. 4.Уравнение прямой. 5.Координаты точки пересечения.	1.Площадь прямоугольника. 2.Площадь параллелограмма. 3.Площадь треугольника. 4.Площадь круга. 5.Площадь подобных фигур. 6.Площадь трапеции.

www.mathtask.ru

Египетский треугольник и обратная теорема Пифагора – Fib0.ru – Суть числа

Обратная Теорема Пифагора

Математический лайфхак из обасти геометрии “Как при помощи простой верёвки получить треугольник с прямым углом”.
Египтяне 4000 лет назад для строительства пирамид использовали метод получения прямоугольного треугольника при помощи верёвки разделенной на 12 равных частей.

Понятие “египетский треугольник”.

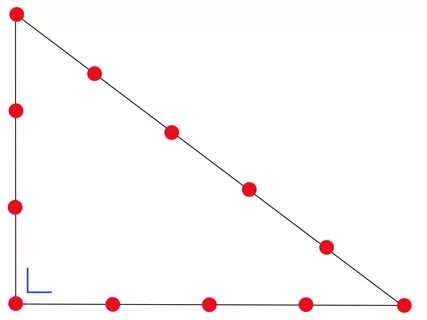Египетский треугольник

Почему треугольник со сторонами 3, 4, 5 называют египетским?

А всё дело в том, что строителям Древнего Египта пирамид нужен был простой и надежный метод построения треугольника с прямым углом. И вот как они это реализовывали. Верёвку разбивали на двеадцать равновеликих частей, обозначив границы между соседними частями; концы верёвки соединяли. После этого 3 человека натягивали верёвку таким образом, чтобы она образовала треугольник, причем расстояния между каждыми двумя египтянами, тянущими веревку, составляли соответственно три части, четыре части и пять частей. Получался треугольник с прямым углом с катетами в три и четыре части и гипотенузой в пять частей. Известно, прямым был угол между сторонами в три и четыре части. Как известно, древнеегипетских землемеров, которые кроме обмеривания земельных наделов занимались построениями на местности, в древнем Египте их называли гарпедонаптами (что буквально переводится как «натягивающие верёвки»). Гарпедонапты занимали 3 место в иерархии жрецоы Древнего Египта.

Обратная теорема Пифагора.

Но из-за чего треугольник со сторонами 3, 4, 5 окажется прямоугольным? Большинство ответили бы на данный вопрос, что данный факт это теорема Пифагора: так как три в квадрате плюс четыре в квадрате равняется пяти в квадрате. Но теорема Пифагора говорит, что если треугольник с прямым углом, то тогда сумма квадратов 2-х его сторон равняется квадрату третьей. Здесь мы имеем дело с теоремой, обратной теореме Пифагора: если сумма квадратов 2-х сторон треугольника равна квадрату третьей, то тогда треугольник — прямоугольный.

Обрисованное практическое приложение обратной теоремы Пифагора относиться к далёкому прошлому. Едва ли кто-либо получает прямые углы таким методом сегодня. Но тем не менее данный способ является отличным математическим лайфхаком и может быть применён Вами в любой жизненной ситуации.

Метод определения прямоугольного треугольника при помощи верёвки из мира практики переместился в мир идей, подобно тому как многое из материальной культуры древности вошло в духовную культуру нынешней действительности.

fib0.ru

«КОСМИЧЕСКИЙ ГОСТ»: Часть V. САКРАЛЬНАЯ ГЕОМЕТРИЯ И СИМВОЛЫ ТРАДИЦИИ

Передача Учения посредством символов может быть настолько же эффективна, как и при помощи слов. Многие символы, используемые современными масонами, были ими унаследованы от средневековых орденов Мастеров-Строителей, которые закодировали в символах соотношения, почитающиеся сакральными.

Корни из 2, 3 и 5

Всем известный герб Строителей – перекрещенные циркуль и угольник – символизируют два основных принципа священной геометрии – Ad Triangulum и Ad Quadratum – «от треугольника» и «от квадрата» и соответствующие им пропорции корня из 2 и корня из 3. Циркуль раскрыт под углом 60 градусов – таким же, как у вершин равностороннего треугольника, а угольник, как и полагается, имеет угол 90 градусов – как углы квадрата. (Вообще, в символической форме сакральные пропорции чаще выражались при помощи углов, нежели при помощи соотношений длины).

На нижеприведенной иллюстрации — герб Строителей, для наглядности помещенный на фоне чертежа готического Миланского собора, в котором были материализованы принципы «от треугольника» и «от квадрата»:

Золотой треугольник

А вот в этом масонском шевроне, помимо корня из 2 и корня из 3, также отражена пропорция золотого сечения:

Pавнобедренный треугольник, внутри которого изображено «Всевидящее Око», имеет угол при вершине в 108 градусов. Это «большой золотой треугольник», названный так потому, что соотношение между каждой из его сторон и основанием является золотым сечением. Треугольники с углом 108 градусов являются составными частями пентаграммы, которая по сути вся состоит из пропорций золотого сечения:

В других образцах символики Строителей со «Всевидящим Оком», однако, изображение глаза помещено в треугольник (точнее, пирамиду) с углом при вершине в 45 градусов. Таким образом, вместо золотого сечения символ содержит пропорцию корня из 2 (диагональ делит квадрат на два треугольника с углами при основаниях в 45 градусов).

Восемь равносторонних треугольников с углом при вершине в 45 градусов (аналогичных треугольнику на данном символе) образуют октагон.

«Всевидящее Око» — Vesica Piscis

Что касается геометрической символики самого «Всевидящего Ока», то она имеет отношение к основе основ науки Строителей, «матери» всех Божественных пропорций – так называемому Vesica Piscis – «рыбьему пузырю» или «глазу», образующемуся на пересечении двух окружностей одинакового диаметра.

Сакральная геометрия начинается с Vesica Piscis. Как мы уже наблюдали в предыдущем разделе «Космического ГОСТа», Части IV о корнях, на пересечении двух окружностей рождаются две главные формы Строителей – квадрат и равносторонний треугольник, а также сразу три базовые пропорции: корень из 2, корень из 3 и корень из 5.

Раннее христианство придавало очень большое значение Vesica Piscis, это был один из символов Христа. Согласно одной из мистических трактовок, Христос («Сын Человеческий») рождается на пересечении круга Божественного с кругом человеческого.

Раннехристианская архитектура (в час

assalam786.livejournal.com

Египетский треугольник

Очень важно, чтобы материал, с которым учащиеся познакомятся на уроке, вызвал у них интерес.

О теореме Пифагора

Уделом истины не может быть забвенье,
Как только мир ее увидит взор,
И теорема та, что дал нам Пифагор,
Верна теперь, как в день ее рожденья.
За светлый луч с небес вознес благодаренье
Мудрец богам не так, как было до тех пор.
Ведь целых сто быков послал он под топор,
Чтоб их сожгли как жертвоприношенье.

Быки с тех пор, как только весть услышат,
Что новой истины уже следы видны,
Отчаянно мычат и ужаса полны:
Им Пифагор навек внушил тревогу.
Не в силах преградить той истине дорогу,
Они, закрыв глаза, дрожат и еле дышат.
(А. фон Шамиссо, перевод Хованского)

Пифагор, VI в. до н. э. (580 – 500), древнегреческий философ и математик. Первым заложил основы математики как науки, имел свою школу (школа Пифагора). Ему приписывают и открытие так называемой теоремы Пифагора, хотя геометрическая интерпретация этой проблемы была известна и раньше.

Задача на смекалку

Поликрат (известный из баллады Шиллера тиран с острова Самос) однажды спросил на пиру у Пифагора, сколько у того учеников. “Охотно скажу тебе, о Поликрат, — отвечал Пифагор. – Половина моих учеников изучает прекрасную математику. Четверть исследует тайны вечной природы. Седьмая часть молча упражняет силу духа, храня в сердце учение. Добавь еще к ним трех юношей, из которых Теон превосходит прочих своими способностями. Столько учеников веду я к рождению вечной истины”. Сколько учеников было у Пифагора?

РЕШЕНИЕ:

Пусть х – число учеников Пифагора.

По условию задачи составим уравнение:

ОТВЕТ: 28 учеников.

Начнем урок в школе Пифагора.

1. Практическая работа

(Несколько человек работают у доски, остальные в тетрадях).

Задание 1. Построить треугольник по трем сторонам, если стороны равны.

а) 3, 4, 5;

б) 6, 8, 10;

в) 5, 12, 13 (единицы измерения указывать не обязательно).

Задание 2. Измерить больший угол этих треугольников.

Ответы близки к 90^о.
Учитель предлагает внимательно посмотреть на построенные треугольники, найти отличия и определить, чем эти треугольники похожи друг на друга. Класс постепенно находит нужную формулировку: “Если треугольник имеет стороны a, b, c и a²+b²=c², то угол, противолежащий стороне с, прямой”.
Доказательство этой теоремы – обратной к теореме Пифагора.
2. Устная работа

1) в прямоугольном треугольнике гипотенуза и катет соответственно равны 13 и 5. Найдите второй катет.

2) в прямоугольном треугольнике катеты равны 1,5 и 2. Найдите гипотенузу.

3) определите вид треугольника, стороны которого равны 6, 8, 10.

3. Практическая работа

На тонкой веревке делают метрии, делящие ее на 12 равных частей, связывают концы, а затем растягивают веревку в виде треугольника со сторонами 3, 4, 5. Тогда угол между сторонами 3 и 4 оказывается прямым.
ВЫВОД: если стороны треугольника пропорциональны числам 3, 4 и 5, то этот треугольник прямоугольный.
Учитель говорит учащимся, что этот факт использовался египтянами для построения на местности прямых углов – ведь оптических измерительных приборов тогда еще не было, а для строительства домов, дворцов и тем более гигантских пирамид надо было уметь строить прямые углы.
(Звучит музыка. Демонстрация слайдов с изображением античных дворцов, храмов, египетских пирамид).
Перед тем как перейти к следующему этапу урока, ученики вместе с учителем еще раз делают вывод, что безошибочность построения прямых углов следует из теоремы, обратной к теореме Пифагора. Проверяют еще раз эту теорему на треугольнике со сторонами 3, 4, 5: 3² + 4² = 5². Далее можно сказать, что в общем виде уравнение записывается следующим образом: а² + b² = с². Необходимо проверить есть ли еще корни у этого уравнения.
Учащиеся проверяют этот факт. Прямоугольными являются также треугольники со сторонами:
5, 12, 13;

8, 15, 17;

7, 24, 25.

Далее учитель сообщает, что прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.
Учитель предлагает тем учащимся, которых заинтересовала данная тема, дома доказать, что катеты a, b и гипотенуза с таких треугольников выражаются формулами:
а = 2mn, b = m² — n², c = m² + n²,
где m и n – любые натуральные числа, такие, что m > n.
В финале урока уместно прочитать известные стихи, посвященные теореме Пифагора.

Теорема Пифагора

Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
(И. Дырченко)

urok.1sept.ru
Треугольник. Формулы и свойства треугольников.

Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.

Типы треугольников
По величине углов
Остроугольный треугольник — все углы треугольника острые.
Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
По числу равных сторон
Разносторонний треугольник — все три стороны не равны.
Равнобедренный треугольник — две стороны равны.
Равносторонним треугольник или правильный треугольник — все три стороны равны.

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника

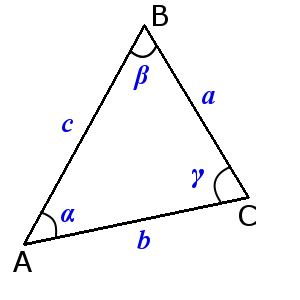
Сумма углов треугольника равна 180°:
α + β + γ = 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β, тогда a > b
если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
a = b = c = 2R
sin α sin β sin γ
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a² = b² + c² — 2bc·cos α
b² = a² + c² — 2ac·cos β
c² = a² + b² — 2ab·cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианы
a = 23√2(m_b² + m_c²) — m_a²
b = 23√2(m_a² + m_c²) — m_b²
c = 23√2(m_a² + m_b²) — m_c²

Медианы треугольника

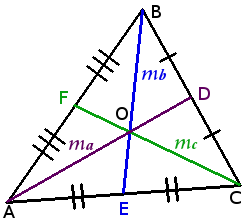
Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
Медианы треугольника пересекаются в одной точке. (Точка пересечения медиан называется центроидом)

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AOOD = BOOE = COOF = 21

Медиана треугольника делит треугольник на две равновеликие части
S_∆ABD = S_∆ACD
S_∆BEA = S_∆BEC
S_∆CBF = S_∆CAF

Треугольник делится тремя медианами на шесть равновеликих треугольников.
S_∆AOF = S_∆AOE = S_∆BOF = S_∆BOD = S_∆COD = S_∆COE

Из векторов, образующих медианы, можно составить треугольник.

Формулы медиан треугольника
Формулы медиан треугольника через стороны
m_a = 12√2b²+2c²-a²
m_b = 12√2a²+2c²-b²
m_c = 12√2a²+2b²-c²

Биссектрисы треугольника

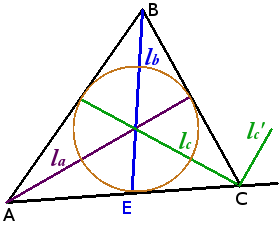
Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника:
Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AEAB = ECBC

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Угол между l_c и l_c‘ = 90°

Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.

Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
l_a = 2√bcp(p — a)b + c
l_b = 2√acp(p — b)a + c
l_c = 2√abp(p — c)a + b
где p = a + b + c2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
l_a = 2bc cos α2b + c
l_b = 2ac cos β2a + c
l_c = 2ab cos γ2a + b

Высоты треугольника

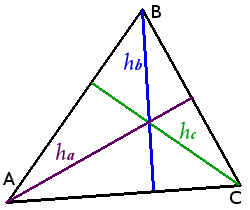
Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться
внутри треугольника — для остроугольного треугольника;

совпадать с его стороной — для катета прямоугольного треугольника;

проходить вне треугольника — для острых углов тупоугольного треугольника.

Свойства высот треугольника
Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.
h_a:h_b:h_c = 1a:1b:1c = (bc):(ac):(ab)
Формулы высот треугольника
Формулы высот треугольника через сторону и угол:
h_a = b sin γ = c sin β
h_b = c sin α = a sin γ
h_c = a sin β = b sin α
Формулы высот треугольника через сторону и площадь:
h_a = 2Sa
h_b = 2Sb
h_c = 2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности:
h_a = bc2R
h_b = ac2R
h_c = ab2R

Окружность вписанная в треугольник

Определение. Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру: Радиус вписанной в треугольник окружности через три стороны:
r = (a + b — c)(b + c — a)(c + a — b)4(a + b + c)
Радиус вписанной в треугольник окружности через три высоты:
Окружность описанная вокруг треугольника

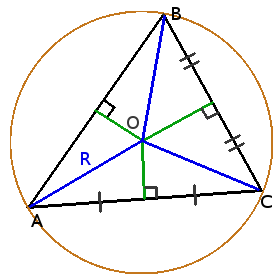
Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Центр вписанной в треугольник окружности лежит на пересечении серединных перпендикуляров к уго сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь: Радиус описанной окружности через площадь и три угла:
R = S2 sin α sin β sin γ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов):
R = a2 sin α = b2 sin β = c2 sin γ

Связь между вписанной и описанной окружностями треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то.
rR = 4 sinα2sinβ2sinγ2 = cos α + cos β + cos γ — 1

Средняя линия треугольника
Определение. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
1. Любой треугольник имеет три средних линии
2.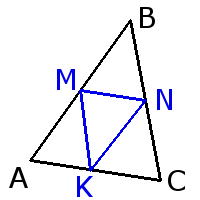 Средняя линия треугольника параллельна основанию и равна его половине.
MN = 12AC KN = 12AB KM = 12BC
MN || AC KN || AB KM || BC
3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольника
S_∆MBN = 14 S_∆ABC
S_∆MAK = 14 S_∆ABC
S_∆NCK = 14 S_∆ABC
4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
∆MBN ∼ ∆ABC
∆AMK ∼ ∆ABC
∆KNC ∼ ∆ABC
∆NKM ∼ ∆ABC
Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.

Периметр треугольника

Периметр треугольника ∆ABC равен сумме длин его сторон
P = a + b + c

Формулы площади треугольника

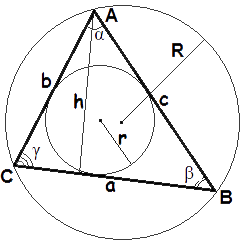
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
S = 12a · h_a
S = 12b · h_b
S = 12c · h_c

Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
где p = a + b + c2 — полупериметр треугльника.

Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 12a · b · sin γ
S = 12b · c · sin α
S = 12a · c · sin β

Формула площади треугольника по трем сторонам и радиусу описанной окружности

Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

Равенство треугольников
Определение. Если два треугольника АВС и А₁В₁С₁ можно совместить наложением, то они равны.
Свойства. У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)
Признаки равенства треугольников
Теорема 1.
Первый признак равенства треугольников — по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Теорема 2.
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Теорема 3.
Третий признак равенства треугольников — по трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Подобие треугольников
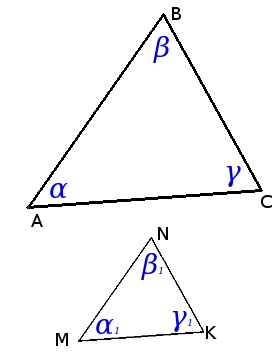Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.
∆АВС ~ ∆MNK => α = α₁, β = β₁, γ = γ₁ и ABMN = BCNK = ACMK = k,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.
Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:
S_∆АВСS_∆MNK = k²

ru.onlinemschool.com
§14. Треугольник и его виды
ПОВТОРЯЕМ ТЕОРИЮ
146. Заполните пропуски.
1) Из всех многоугольников наименьшее количество углов и сторон имеют треугольники.
2) Треугольники можно классифицировать по виду их углов и по количеству равных сторон.
3) По виду углов треугольники бывают остроугольными, прямоугольными, тупоугольными.
4) Остроугольным называют треугольник, у которого все углы острые.
5) Прямоугольным называют треугольник, у которого один угол прямой, т.е. равен 90 градусам.
6) Тупоугольным называют треугольник, у которого один из углов тупой.
7) По количеству равных сторон треугольники делятся на разносторонние, равнобедренные, равносторнние.
8) Равнобедренным называют треугольник, у которого две стороны равны.
9) Равные стороны равнобедренного треугольника называют боковыми сторонами, а его третью сторону называют основанием.
10) Равносторонним называют треугольник, у которого все стороны равны.
11) Периметр равностороннего треугольника со стороной а вычисляют по формуле Р=3-а.
12) Разносторонним называют треугольник, у которого все стороны треугольника разные.

РЕШАЕМ ЗАДАЧИ
147. Определите вид треугольника.
148. Периметр треугольника со сторонами 12 см, 18 см, 24 см равен 54 см.
149. Периметр равностороннего треугольника сто стороной 7 см равен 21 см.
150. Одна сторона треугольника равна 17 см, вторая сторона — на 7 см больше первой, а третья — в 3 раза меньше второй. Вычислите периметр треугольника.
Решение:
1) 17+7=24 (см) длина второй стороны треугольника
2) 24:3=8 (см) третья сторона
3) 17+24+8=49 (см) периметр треугольника
Ответ: периметр треугольника равен 49 см.
151. Найдите периметр равнобедренного треугольника, основание которого равно 9 см, а боковая сторона — 6 см.
Решение:
Р=9+6*2=9+12=21 (см)
Ответ: периметр треугольника равен 21 см.
152. С помощью линейки и транспортира постройте треугольник и укажите его вид, если:
1) две стороны равны 2 см и 3 см, а угол между ними 50 градусов.
2) две стороны равны 4 см и 2 см 5 мм, а угол между ними — 100 градусов.
3) две стороны равны 1 см и 3 см, а угол между ними — 90 градусов.
4) две стороны равны по 2 см 5 мм, а угол между ними — 70 градусов.
5) две стороны равны по 2 см, а угол между ними — 60 градусов.
6) одна сторона равна 4 см 5 мм, а углы, прилежащие к этой стороне — 20 и 80 градусов.
7) одна сторона равна 1 см, а углы, прилежащие к этой стороне, — 110 и 50 градусов.
8) одна сторона равна 2 см, а углы, прилежащие к этой стороне, — 90 и 45 градусов.
9) одна сторона равна 3 см, а углы, прилежащие к этой стороне, — по 30 градусов.
10) одна сторона равна 4 см, а углы, прилежащие к этой стороне, — по 45 градусов.
153. Из скольких одинаковых палочек нельзя сложить треугольник (палочки ломать нельзя): 1) 7, 2) 6, 3) 5, 4) 4?
1) можно: 2, 2, 3.
2) можно: 2, 2, 2.
3) моно: 2, 2, 1.
4) нельзя.
matem-gdz.ru
No related posts.